Decomposition Techniques for Subgraph Matching
Paper and Code
May 07, 2008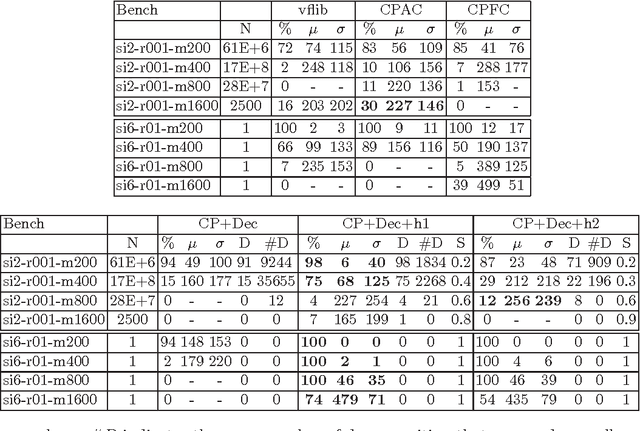
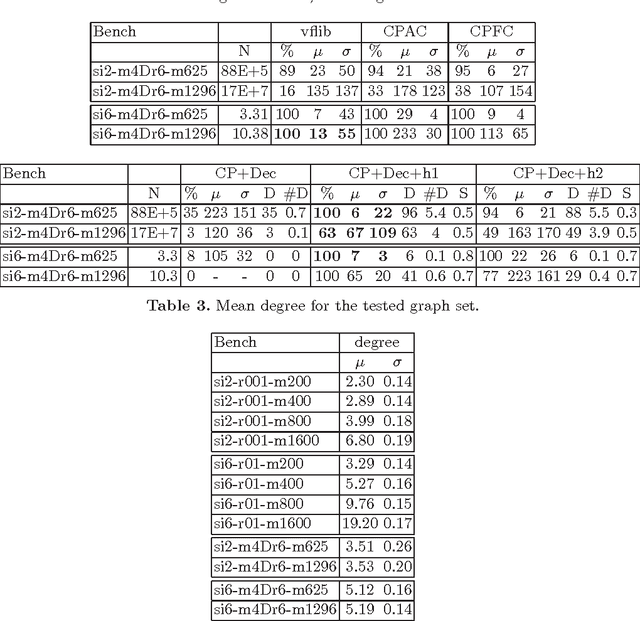
In the constraint programming framework, state-of-the-art static and dynamic decomposition techniques are hard to apply to problems with complete initial constraint graphs. For such problems, we propose a hybrid approach of these techniques in the presence of global constraints. In particular, we solve the subgraph isomorphism problem. Further we design specific heuristics for this hard problem, exploiting its special structure to achieve decomposition. The underlying idea is to precompute a static heuristic on a subset of its constraint network, to follow this static ordering until a first problem decomposition is available, and to switch afterwards to a fully propagated, dynamically decomposing search. Experimental results show that, for sparse graphs, our decomposition method solves more instances than dedicated, state-of-the-art matching algorithms or standard constraint programming approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge