Decomposition of Nonlinear Dynamical Systems Using Koopman Gramians
Paper and Code
Oct 04, 2017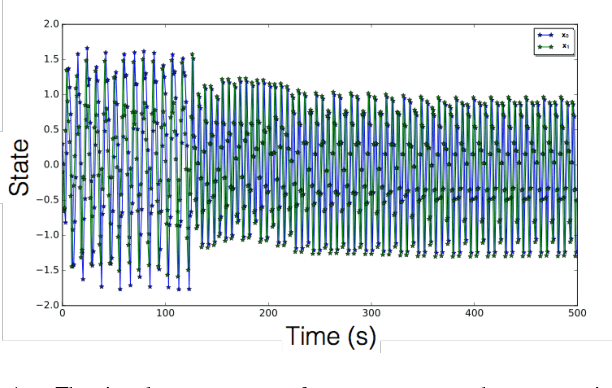
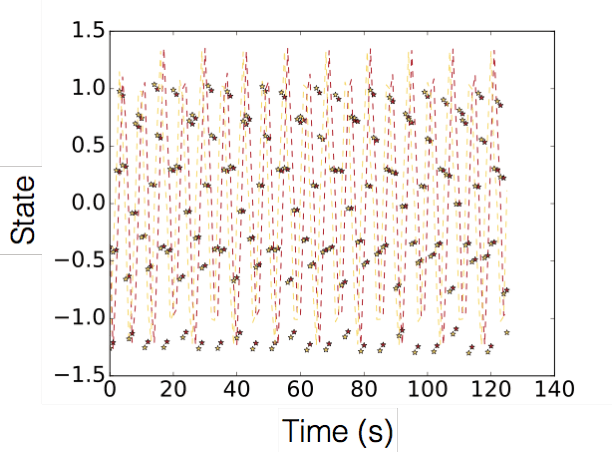

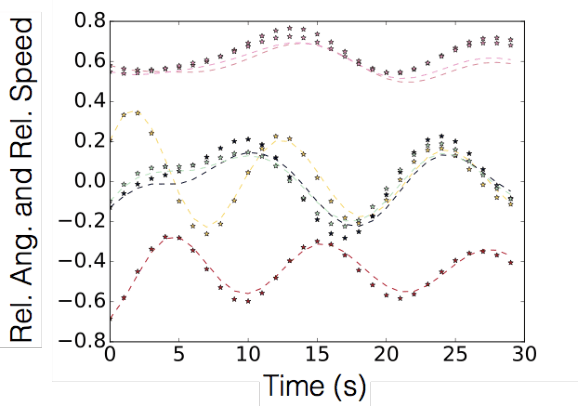
In this paper we propose a new Koopman operator approach to the decomposition of nonlinear dynamical systems using Koopman Gramians. We introduce the notion of an input-Koopman operator, and show how input-Koopman operators can be used to cast a nonlinear system into the classical state-space form, and identify conditions under which input and state observable functions are well separated. We then extend an existing method of dynamic mode decomposition for learning Koopman operators from data known as deep dynamic mode decomposition to systems with controls or disturbances. We illustrate the accuracy of the method in learning an input-state separable Koopman operator for an example system, even when the underlying system exhibits mixed state-input terms. We next introduce a nonlinear decomposition algorithm, based on Koopman Gramians, that maximizes internal subsystem observability and disturbance rejection from unwanted noise from other subsystems. We derive a relaxation based on Koopman Gramians and multi-way partitioning for the resulting NP-hard decomposition problem. We lastly illustrate the proposed algorithm with the swing dynamics for an IEEE 39-bus system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge