Decision fusion with multiple spatial supports by conditional random fields
Paper and Code
Aug 24, 2018

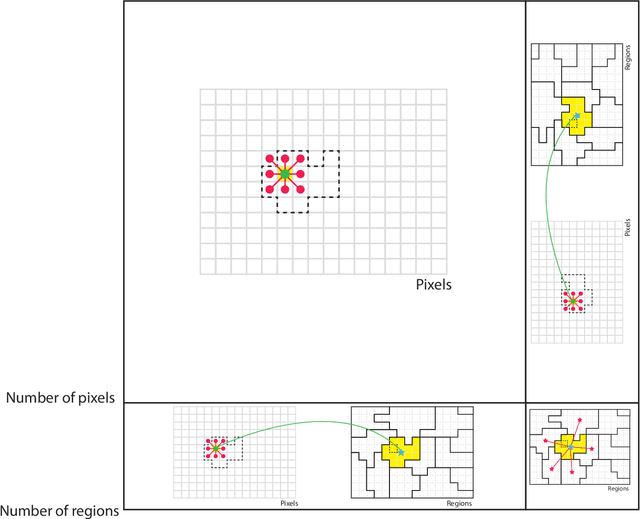

Classification of remotely sensed images into land cover or land use is highly dependent on geographical information at least at two levels. First, land cover classes are observed in a spatially smooth domain separated by sharp region boundaries. Second, land classes and observation scale are also tightly intertwined: they tend to be consistent within areas of homogeneous appearance, or regions, in the sense that all pixels within a roof should be classified as roof, independently on the spatial support used for the classification. In this paper, we follow these two observations and encode them as priors in an energy minimization framework based on conditional random fields (CRFs), where classification results obtained at pixel and region levels are probabilistically fused. The aim is to enforce the final maps to be consistent not only in their own spatial supports (pixel and region) but also across supports, i.e., by getting the predictions on the pixel lattice and on the set of regions to agree. To this end, we define an energy function with three terms: 1) a data term for the individual elements in each support (support-specific nodes); 2) spatial regularization terms in a neighborhood for each of the supports (support-specific edges); and 3) a regularization term between individual pixels and the region containing each of them (intersupports edges). We utilize these priors in a unified energy minimization problem that can be optimized by standard solvers. The proposed 2LCRF model consists of a CRF defined over a bipartite graph, i.e., two interconnected layers within a single graph accounting for interlattice connections.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge