Decision Forest: A Nonparametric Approach to Modeling Irrational Choice

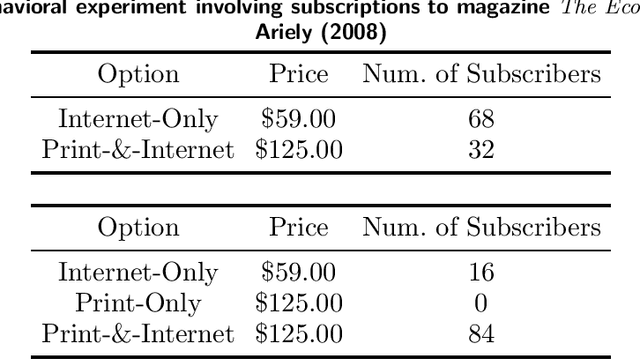
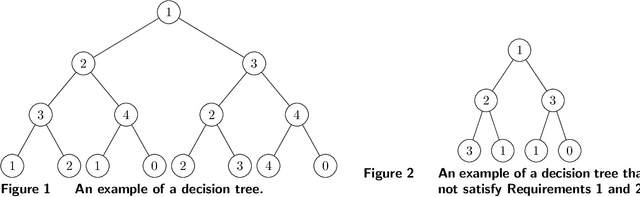
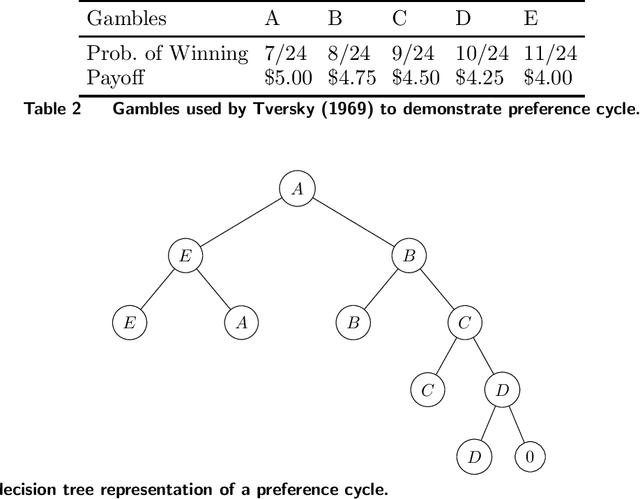
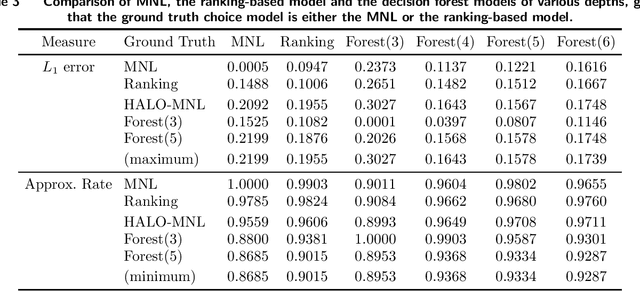
Customer behavior is often assumed to follow weak rationality, which implies that adding a product to an assortment will not increase the choice probability of another product in that assortment. However, an increasing amount of research has revealed that customers are not necessarily rational when making decisions. In this paper, we study a new nonparametric choice model that relaxes this assumption and can model a wider range of customer behavior, such as decoy effects between products. In this model, each customer type is associated with a binary decision tree, which represents a decision process for making a purchase based on checking for the existence of specific products in the assortment. Together with a probability distribution over customer types, we show that the resulting model -- a decision forest -- is able to represent any customer choice model, including models that are inconsistent with weak rationality. We theoretically characterize the depth of the forest needed to fit a data set of historical assortments and prove that asymptotically, a forest whose depth scales logarithmically in the number of assortments is sufficient to fit most data sets. We also propose an efficient algorithm for estimating such models from data, based on combining randomization and optimization. Using synthetic data and real transaction data exhibiting non-rational behavior, we show that the model outperforms the multinomial logit and ranking-based models in out-of-sample predictive ability.