Decentralized Reinforcement Learning: Global Decision-Making via Local Economic Transactions
Paper and Code
Jul 05, 2020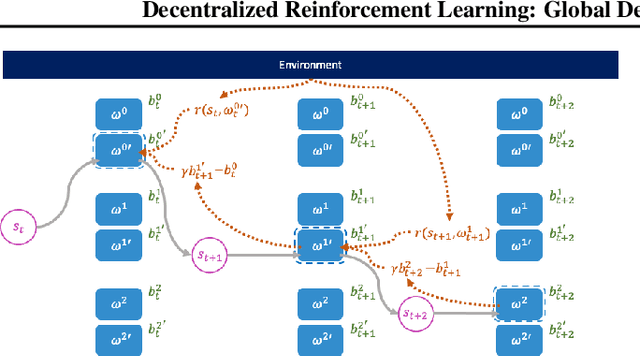
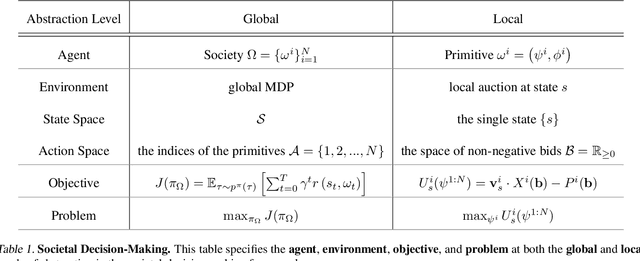
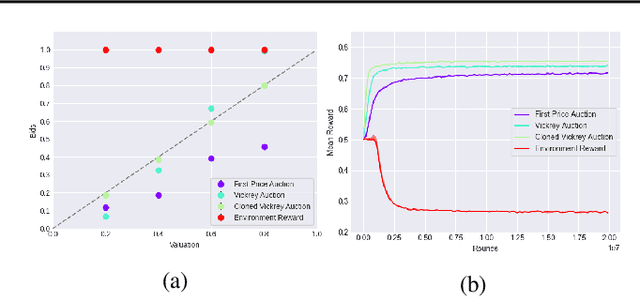
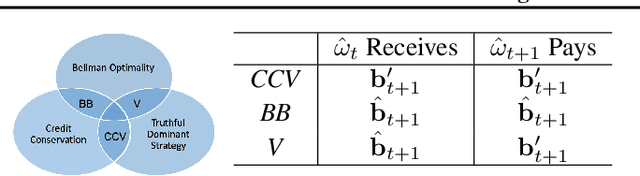
This paper seeks to establish a framework for directing a society of simple, specialized, self-interested agents to solve what traditionally are posed as monolithic single-agent sequential decision problems. What makes it challenging to use a decentralized approach to collectively optimize a central objective is the difficulty in characterizing the equilibrium strategy profile of non-cooperative games. To overcome this challenge, we design a mechanism for defining the learning environment of each agent for which we know that the optimal solution for the global objective coincides with a Nash equilibrium strategy profile of the agents optimizing their own local objectives. The society functions as an economy of agents that learn the credit assignment process itself by buying and selling to each other the right to operate on the environment state. We derive a class of decentralized reinforcement learning algorithms that are broadly applicable not only to standard reinforcement learning but also for selecting options in semi-MDPs and dynamically composing computation graphs. Lastly, we demonstrate the potential advantages of a society's inherent modular structure for more efficient transfer learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge