Decentralized Multi-target Tracking with Multiple Quadrotors using a PHD Filter
Paper and Code
Dec 04, 2020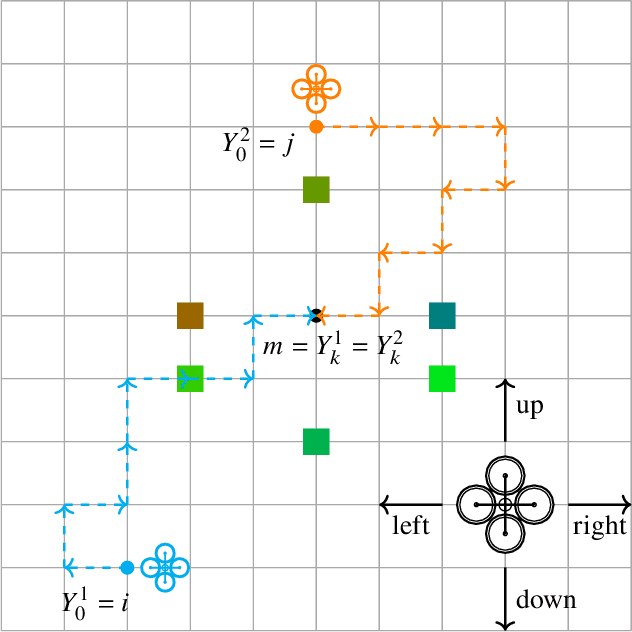

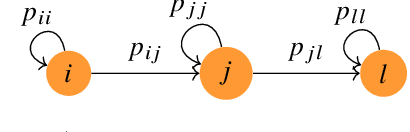
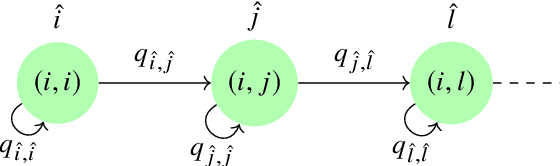
We consider a scenario in which a group of quadrotors is tasked at tracking multiple stationary targets in an unknown, bounded environment. The quadrotors search for targets along a spatial grid overlaid on the environment while performing a random walk on this grid modeled by a discrete-time discrete-state (DTDS) Markov chain. The quadrotors can transmit their estimates of the target locations to other quadrotors that occupy their current location on the grid; thus, their communication network is time-varying and not necessarily connected. We model the search procedure as a renewal-reward process on the underlying DTDS Markov chain. To accommodate changes in the set of targets observed by each quadrotor as it explores the environment, along with uncertainties in the quadrotors' measurements of the targets, we formulate the tracking problem in terms of Random Finite Sets (RFS). The quadrotors use RFS-based Probability Hypothesis Density (PHD) filters to estimate the number of targets and their locations. We present a theoretical estimation framework, based on the Gaussian Mixture formulation of the PHD filter, and preliminary simulation results toward extending existing approaches for RFS-based multi-target tracking to a decentralized multi-robot strategy for multi-target tracking. We validate this approach with simulations of multi-target tracking scenarios with different densities of robots and targets, and we evaluate the average time required for the robots in each scenario to reach agreement on a common set of targets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge