Debiasing Conditional Stochastic Optimization
Paper and Code
Apr 20, 2023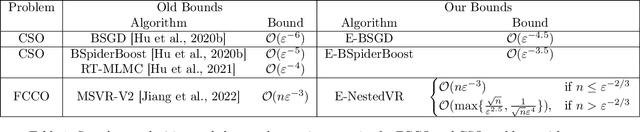
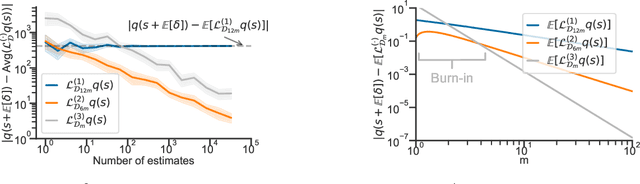
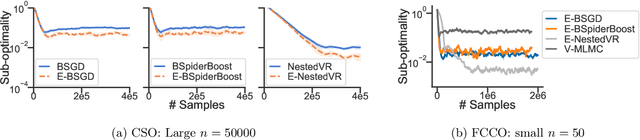
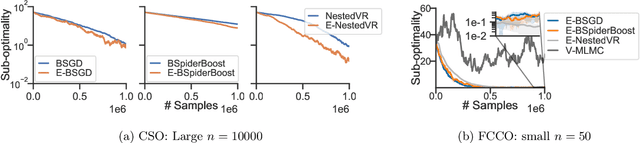
In this paper, we study the conditional stochastic optimization (CSO) problem which covers a variety of applications including portfolio selection, reinforcement learning, robust learning, causal inference, etc. The sample-averaged gradient of the CSO objective is biased due to its nested structure and therefore requires a high sample complexity to reach convergence. We introduce a general stochastic extrapolation technique that effectively reduces the bias. We show that for nonconvex smooth objectives, combining this extrapolation with variance reduction techniques can achieve a significantly better sample complexity than existing bounds. We also develop new algorithms for the finite-sum variant of CSO that also significantly improve upon existing results. Finally, we believe that our debiasing technique could be an interesting tool applicable to other stochastic optimization problems too.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge