Data-driven Enhancement of the Time-domain First-order Regular Perturbation Model
Paper and Code
Oct 11, 2022


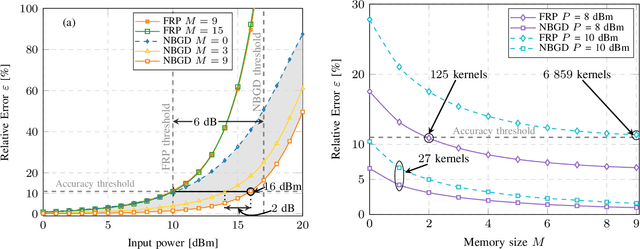
A normalized batch gradient descent optimizer is proposed to improve the first-order regular perturbation coefficients of the Manakov equation, often referred to as kernels. The optimization is based on the linear parameterization offered by the first-order regular perturbation and targets enhanced low-complexity models for the fiber channel. We demonstrate that the optimized model outperforms the analytical counterpart where the kernels are numerically evaluated via their integral form. The enhanced model provides the same accuracy with a reduced number of kernels while operating over an extended power range covering both the nonlinear and highly nonlinear regimes. A $6-7$~dB gain, depending on the metric used, is obtained with respect to the conventional first-order regular perturbation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge