Data-driven End-to-end Learning of Pole Placement Control for Nonlinear Dynamics via Koopman Invariant Subspaces
Paper and Code
Aug 16, 2022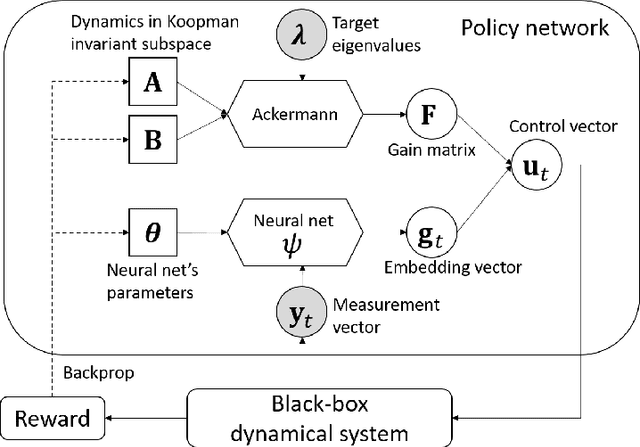

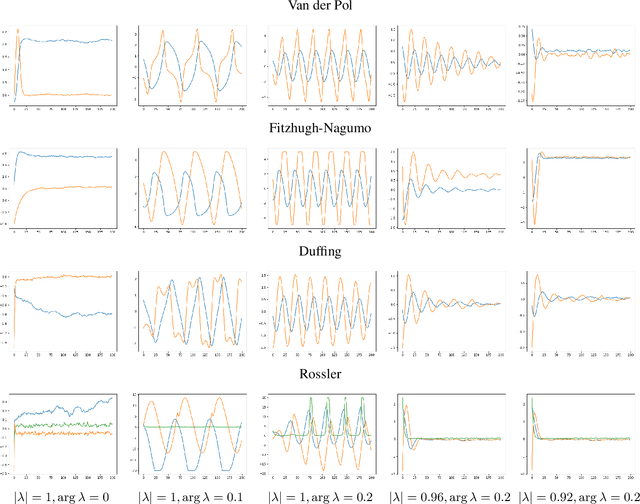
We propose a data-driven method for controlling the frequency and convergence rate of black-box nonlinear dynamical systems based on the Koopman operator theory. With the proposed method, a policy network is trained such that the eigenvalues of a Koopman operator of controlled dynamics are close to the target eigenvalues. The policy network consists of a neural network to find a Koopman invariant subspace, and a pole placement module to adjust the eigenvalues of the Koopman operator. Since the policy network is differentiable, we can train it in an end-to-end fashion using reinforcement learning. We demonstrate that the proposed method achieves better performance than model-free reinforcement learning and model-based control with system identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge