Data Deletion for Linear Regression with Noisy SGD
Paper and Code
Oct 12, 2024


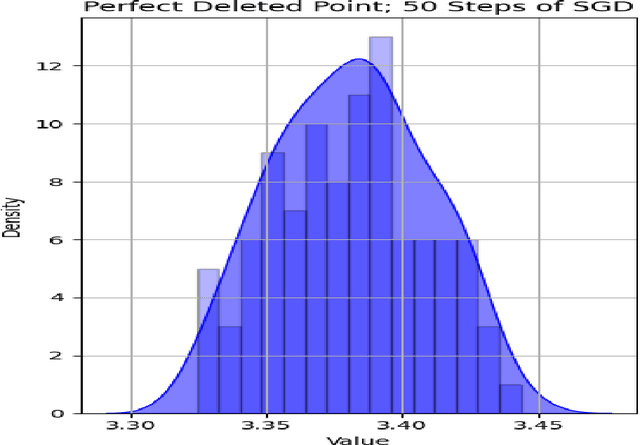
In the current era of big data and machine learning, it's essential to find ways to shrink the size of training dataset while preserving the training performance to improve efficiency. However, the challenge behind it includes providing practical ways to find points that can be deleted without significantly harming the training result and suffering from problems like underfitting. We therefore present the perfect deleted point problem for 1-step noisy SGD in the classical linear regression task, which aims to find the perfect deleted point in the training dataset such that the model resulted from the deleted dataset will be identical to the one trained without deleting it. We apply the so-called signal-to-noise ratio and suggest that its value is closely related to the selection of the perfect deleted point. We also implement an algorithm based on this and empirically show the effectiveness of it in a synthetic dataset. Finally we analyze the consequences of the perfect deleted point, specifically how it affects the training performance and privacy budget, therefore highlighting its potential. This research underscores the importance of data deletion and calls for urgent need for more studies in this field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge