Curved Space Optimization: A Random Search based on General Relativity Theory
Paper and Code
Aug 10, 2012
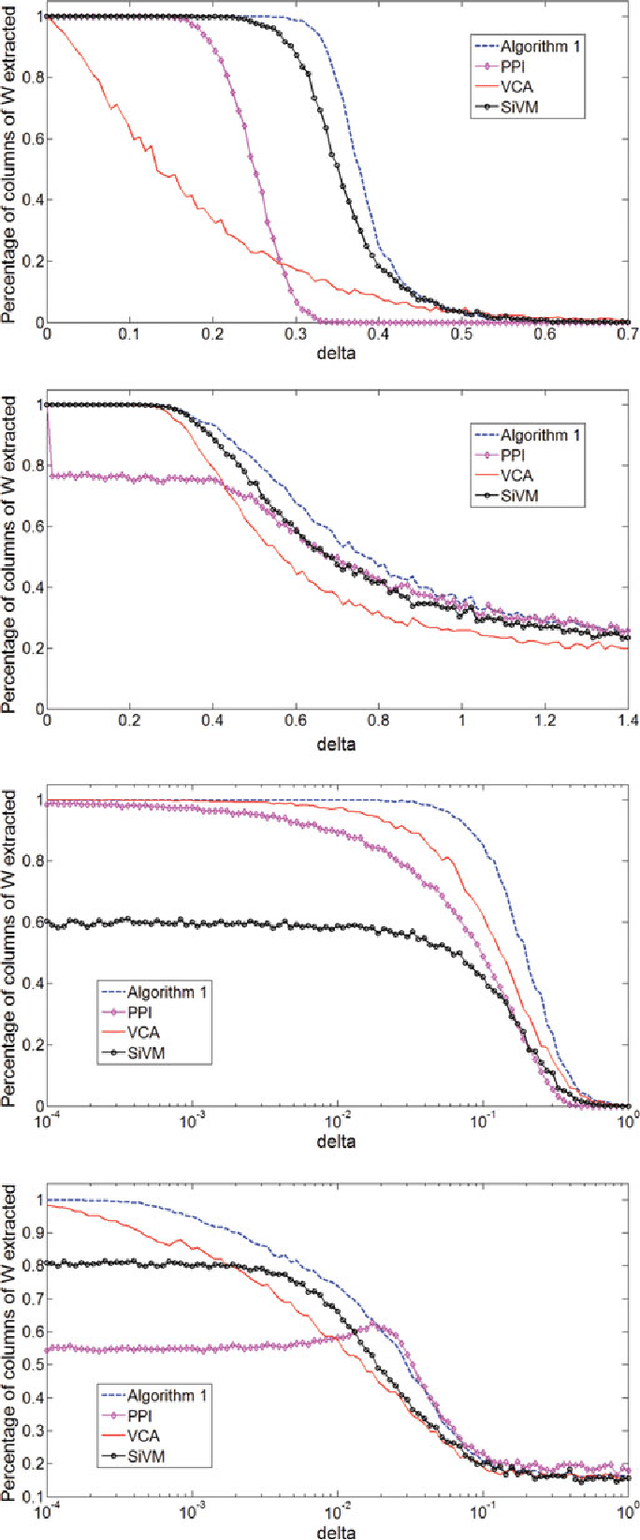
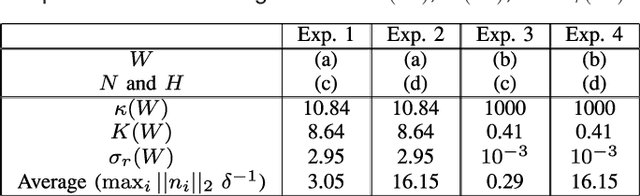
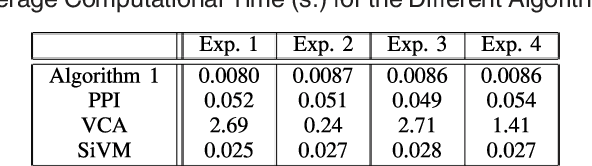
Designing a fast and efficient optimization method with local optima avoidance capability on a variety of optimization problems is still an open problem for many researchers. In this work, the concept of a new global optimization method with an open implementation area is introduced as a Curved Space Optimization (CSO) method, which is a simple probabilistic optimization method enhanced by concepts of general relativity theory. To address global optimization challenges such as performance and convergence, this new method is designed based on transformation of a random search space into a new search space based on concepts of space-time curvature in general relativity theory. In order to evaluate the performance of our proposed method, an implementation of CSO is deployed and its results are compared on benchmark functions with state-of-the art optimization methods. The results show that the performance of CSO is promising on unimodal and multimodal benchmark functions with different search space dimension sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge