Cumulative distribution networks and the derivative-sum-product algorithm
Paper and Code
Jun 13, 2012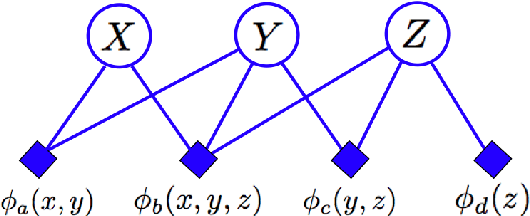

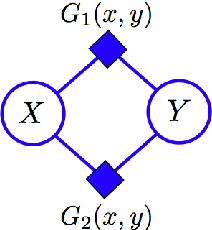

We introduce a new type of graphical model called a "cumulative distribution network" (CDN), which expresses a joint cumulative distribution as a product of local functions. Each local function can be viewed as providing evidence about possible orderings, or rankings, of variables. Interestingly, we find that the conditional independence properties of CDNs are quite different from other graphical models. We also describe a messagepassing algorithm that efficiently computes conditional cumulative distributions. Due to the unique independence properties of the CDN, these messages do not in general have a one-to-one correspondence with messages exchanged in standard algorithms, such as belief propagation. We demonstrate the application of CDNs for structured ranking learning using a previously-studied multi-player gaming dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge