CuMF_SGD: Fast and Scalable Matrix Factorization
Paper and Code
Nov 10, 2016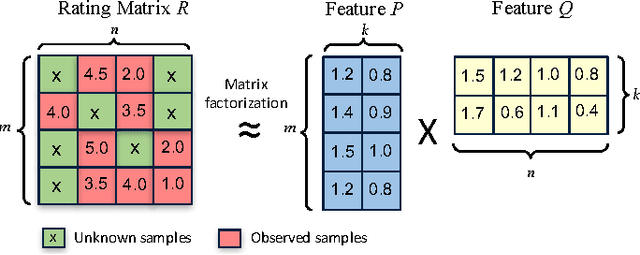
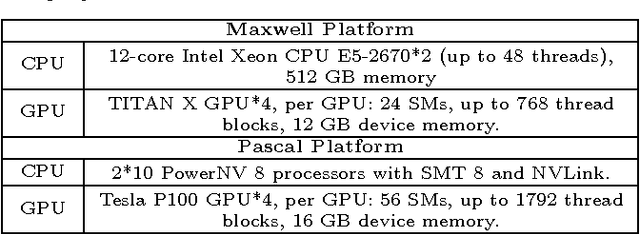
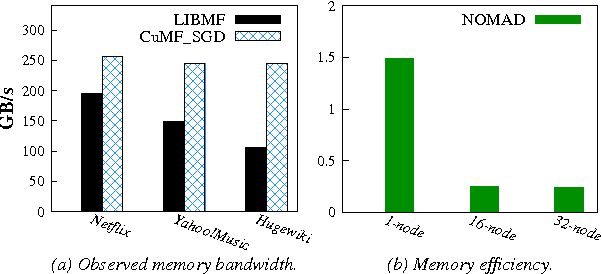
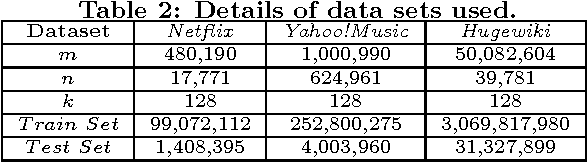
Matrix factorization (MF) has been widely used in e.g., recommender systems, topic modeling and word embedding. Stochastic gradient descent (SGD) is popular in solving MF problems because it can deal with large data sets and is easy to do incremental learning. We observed that SGD for MF is memory bound. Meanwhile, single-node CPU systems with caching performs well only for small data sets; distributed systems have higher aggregated memory bandwidth but suffer from relatively slow network connection. This observation inspires us to accelerate MF by utilizing GPUs's high memory bandwidth and fast intra-node connection. We present cuMF_SGD, a CUDA-based SGD solution for large-scale MF problems. On a single CPU, we design two workload schedule schemes, i.e., batch-Hogwild! and wavefront-update that fully exploit the massive amount of cores. Especially, batch-Hogwild! as a vectorized version of Hogwild! overcomes the issue of memory discontinuity. We also develop highly-optimized kernels for SGD update, leveraging cache, warp-shuffle instructions and half-precision floats. We also design a partition scheme to utilize multiple GPUs while addressing the well-known convergence issue when parallelizing SGD. On three data sets with only one Maxwell or Pascal GPU, cuMF_SGD runs 3.1X-28.2X as fast compared with state-of-art CPU solutions on 1-64 CPU nodes. Evaluations also show that cuMF_SGD scales well on multiple GPUs in large data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge