Critical windows: non-asymptotic theory for feature emergence in diffusion models

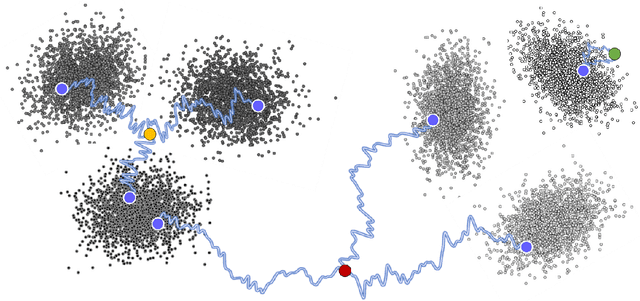
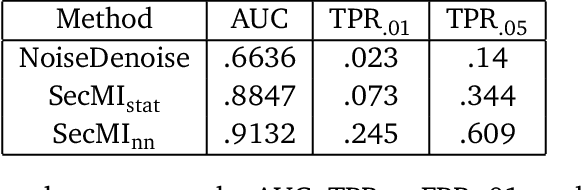
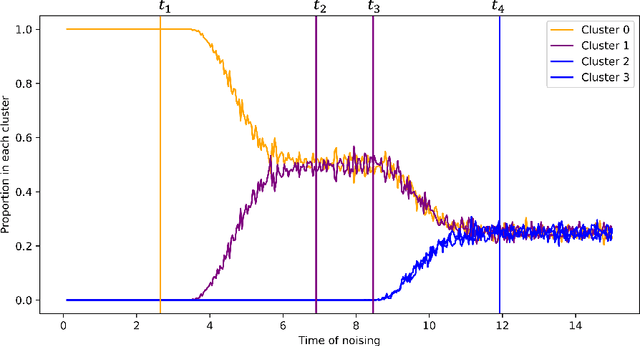
We develop theory to understand an intriguing property of diffusion models for image generation that we term critical windows. Empirically, it has been observed that there are narrow time intervals in sampling during which particular features of the final image emerge, e.g. the image class or background color (Ho et al., 2020b; Georgiev et al., 2023; Raya & Ambrogioni, 2023; Sclocchi et al., 2024; Biroli et al., 2024). While this is advantageous for interpretability as it implies one can localize properties of the generation to a small segment of the trajectory, it seems at odds with the continuous nature of the diffusion. We propose a formal framework for studying these windows and show that for data coming from a mixture of strongly log-concave densities, these windows can be provably bounded in terms of certain measures of inter- and intra-group separation. We also instantiate these bounds for concrete examples like well-conditioned Gaussian mixtures. Finally, we use our bounds to give a rigorous interpretation of diffusion models as hierarchical samplers that progressively "decide" output features over a discrete sequence of times. We validate our bounds with synthetic experiments. Additionally, preliminary experiments on Stable Diffusion suggest critical windows may serve as a useful tool for diagnosing fairness and privacy violations in real-world diffusion models.