CP-PINNs: Changepoints Detection in PDEs using Physics Informed Neural Networks with Total-Variation Penalty
Paper and Code
Aug 18, 2022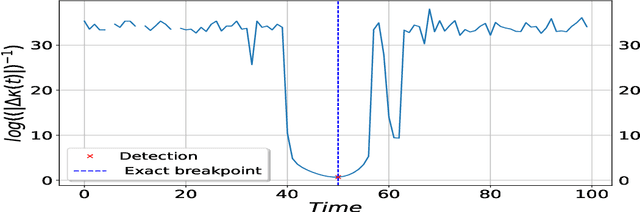
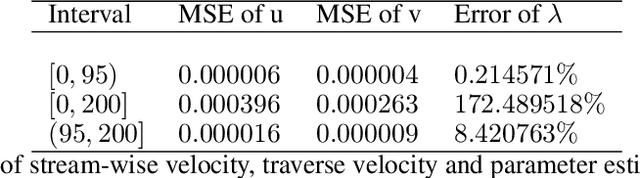
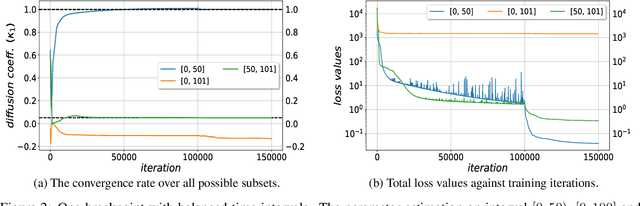
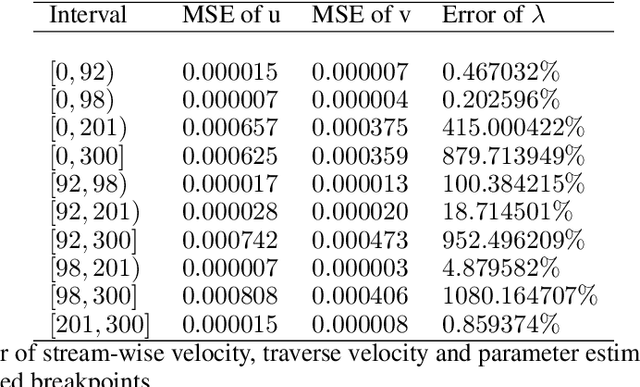
We consider the inverse problem for the Partial Differential Equations (PDEs) such that the parameters of the dependency structure can exhibit random changepoints over time. This can arise, for example, when the physical system is either under malicious attack (e.g., hacker attacks on power grids and internet networks) or subject to extreme external conditions (e.g., weather conditions impacting electricity grids or large market movements impacting valuations of derivative contracts). For that purpose, we employ Physics Informed Neural Networks (PINNs) -- universal approximators that can incorporate prior information from any physical law described by a system of PDEs. This prior knowledge acts in the training of the neural network as a regularization that limits the space of admissible solutions and increases the correctness of the function approximation. We show that when the true data generating process exhibits changepoints in the PDE dynamics, this regularization can lead to a complete miss-calibration and a failure of the model. Therefore, we propose an extension of PINNs using a Total-Variation penalty which accommodates (multiple) changepoints in the PDE dynamics. These changepoints can occur at random locations over time, and they are estimated together with the solutions. We propose an additional refinement algorithm that combines changepoints detection with a reduced dynamic programming method that is feasible for the computationally intensive PINNs methods, and we demonstrate the benefits of the proposed model empirically using examples of different equations with changes in the parameters. In case of no changepoints in the data, the proposed model reduces to the original PINNs model. In the presence of changepoints, it leads to improvements in parameter estimation, better model fitting, and a lower training error compared to the original PINNs model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge