Covariance Recovery for One-Bit Sampled Data With Time-Varying Sampling Thresholds-Part II: Non-Stationary Signals
Paper and Code
Mar 16, 2022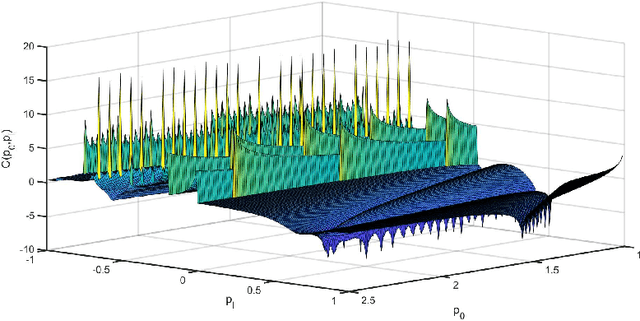
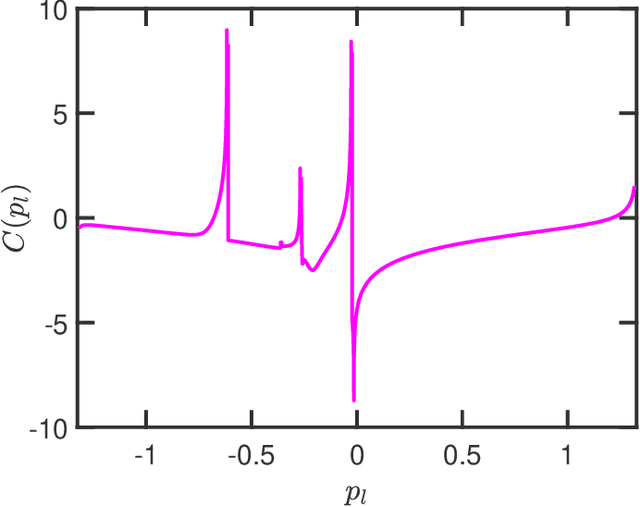
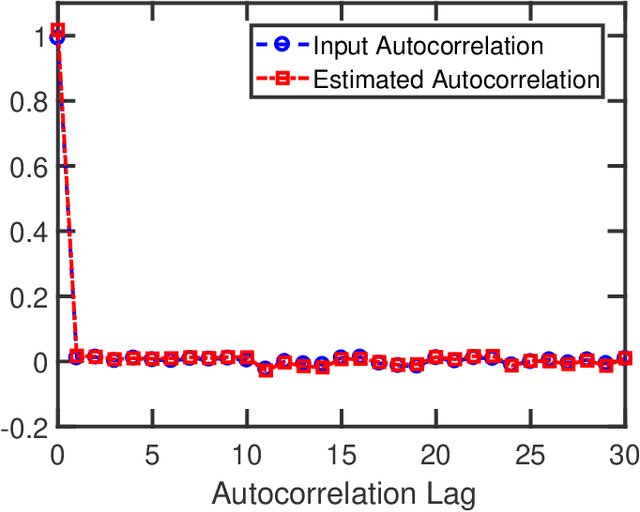
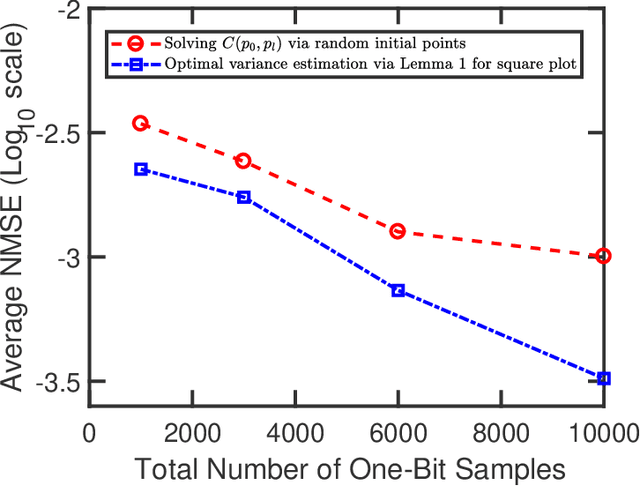
The recovery of the input signal covariance values from its one-bit sampled counterpart has been deemed a challenging task in the literature. To deal with its difficulties, some assumptions are typically made to find a relation between the input covariance matrix and the autocorrelation values of the one-bit sampled data. This includes the arcsine law and the modified arcsine law that were discussed in Part I of this work [2]. We showed that by facilitating the deployment of time-varying thresholds, the modified arcsine law has a promising performance in covariance recovery. However, the modified arcsine law also assumes input signals are stationary, which is typically a simplifying assumption for real-world applications. In fact, in many signal processing applications, the input signals are readily known to be non-stationary with a non-Toeplitz covariance matrix. In this paper, we propose an approach to extending the arcsine law to the case where one-bit ADCs apply time-varying thresholds while dealing with input signals that originate from a non-stationary process. In particular, the recovery methods are shown to accurately recover the time-varying variance and autocorrelation values. Furthermore, we extend the formulation of the Bussgang law to the case where non-stationary input signals are considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge