Covariance Estimation for Matrix-valued Data

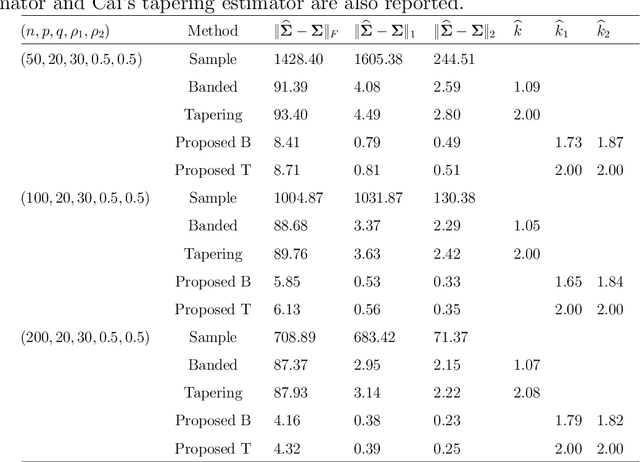
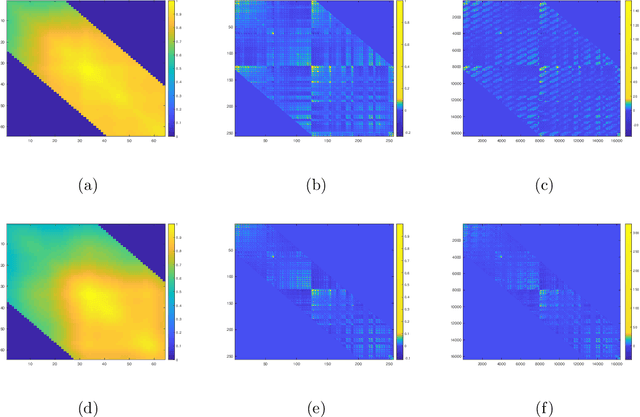
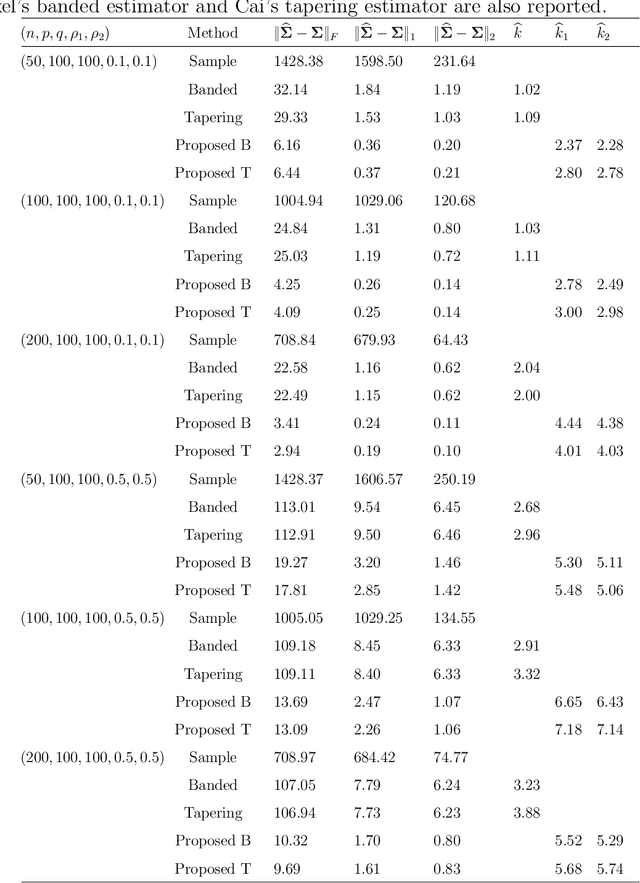
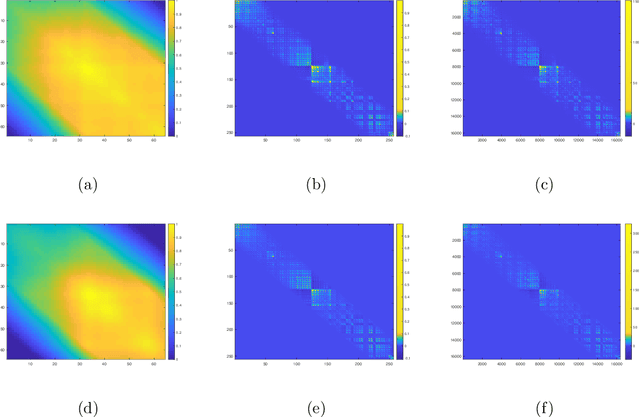
Covariance estimation for matrix-valued data has received an increasing interest in applications including neuroscience and environmental studies. Unlike previous works that rely heavily on matrix normal distribution assumption and the requirement of fixed matrix size, we propose a class of distribution-free regularized covariance estimation methods for high-dimensional matrix data under a separability condition and a bandable covariance structure. Under these conditions, the original covariance matrix is decomposed into a Kronecker product of two bandable small covariance matrices representing the variability over row and column directions. We formulate a unified framework for estimating the banded and tapering covariance, and introduce an efficient algorithm based on rank one unconstrained Kronecker product approximation. The convergence rates of the proposed estimators are studied and compared to the ones for the usual vector-valued data. We further introduce a class of robust covariance estimators and provide theoretical guarantees to deal with the potential heavy-tailed data. We demonstrate the superior finite-sample performance of our methods using simulations and real applications from an electroencephalography study and a gridded temperature anomalies dataset.