Coupled Depth Learning
Paper and Code
Feb 09, 2016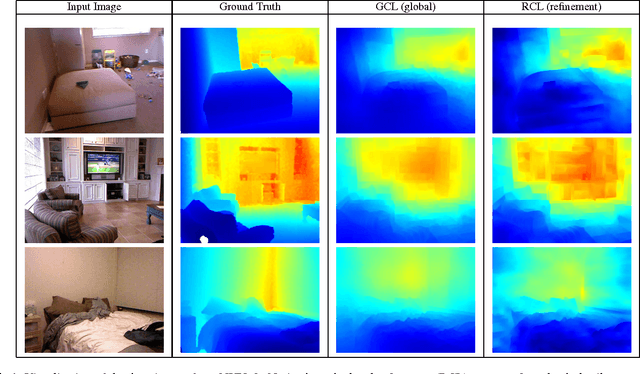


In this paper we propose a method for estimating depth from a single image using a coarse to fine approach. We argue that modeling the fine depth details is easier after a coarse depth map has been computed. We express a global (coarse) depth map of an image as a linear combination of a depth basis learned from training examples. The depth basis captures spatial and statistical regularities and reduces the problem of global depth estimation to the task of predicting the input-specific coefficients in the linear combination. This is formulated as a regression problem from a holistic representation of the image. Crucially, the depth basis and the regression function are {\bf coupled} and jointly optimized by our learning scheme. We demonstrate that this results in a significant improvement in accuracy compared to direct regression of depth pixel values or approaches learning the depth basis disjointly from the regression function. The global depth estimate is then used as a guidance by a local refinement method that introduces depth details that were not captured at the global level. Experiments on the NYUv2 and KITTI datasets show that our method outperforms the existing state-of-the-art at a considerably lower computational cost for both training and testing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge