Counterexample Guided Abstraction Refinement Algorithm for Propositional Circumscription
Paper and Code
Jun 30, 2010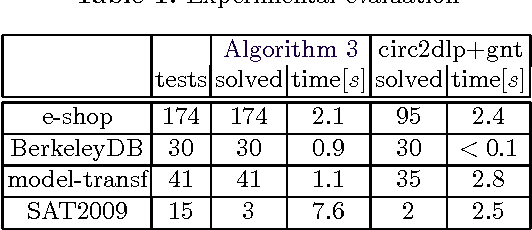
Circumscription is a representative example of a nonmonotonic reasoning inference technique. Circumscription has often been studied for first order theories, but its propositional version has also been the subject of extensive research, having been shown equivalent to extended closed world assumption (ECWA). Moreover, entailment in propositional circumscription is a well-known example of a decision problem in the second level of the polynomial hierarchy. This paper proposes a new Boolean Satisfiability (SAT)-based algorithm for entailment in propositional circumscription that explores the relationship of propositional circumscription to minimal models. The new algorithm is inspired by ideas commonly used in SAT-based model checking, namely counterexample guided abstraction refinement. In addition, the new algorithm is refined to compute the theory closure for generalized close world assumption (GCWA). Experimental results show that the new algorithm can solve problem instances that other solutions are unable to solve.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge