CorrectNet: Robustness Enhancement of Analog In-Memory Computing for Neural Networks by Error Suppression and Compensation
Paper and Code
Nov 27, 2022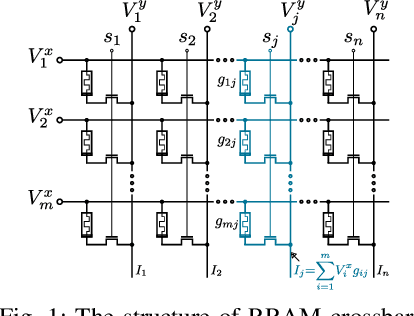
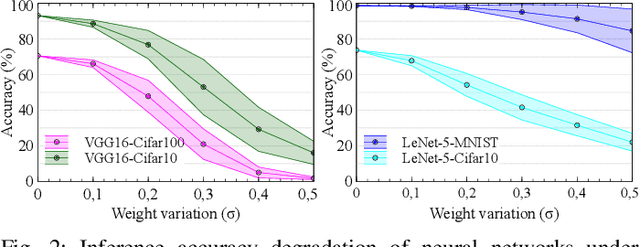
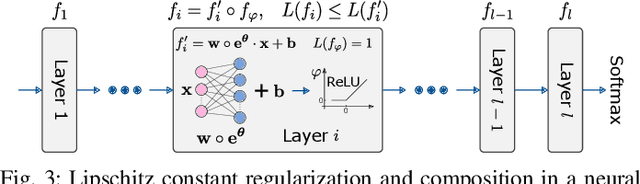
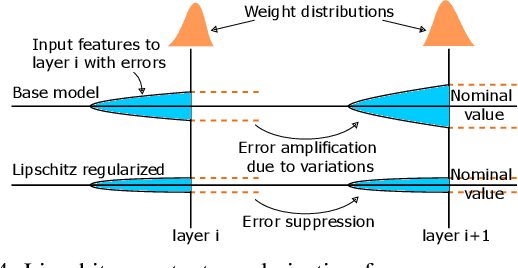
The last decade has witnessed the breakthrough of deep neural networks (DNNs) in many fields. With the increasing depth of DNNs, hundreds of millions of multiply-and-accumulate (MAC) operations need to be executed. To accelerate such operations efficiently, analog in-memory computing platforms based on emerging devices, e.g., resistive RAM (RRAM), have been introduced. These acceleration platforms rely on analog properties of the devices and thus suffer from process variations and noise. Consequently, weights in neural networks configured into these platforms can deviate from the expected values, which may lead to feature errors and a significant degradation of inference accuracy. To address this issue, in this paper, we propose a framework to enhance the robustness of neural networks under variations and noise. First, a modified Lipschitz constant regularization is proposed during neural network training to suppress the amplification of errors propagated through network layers. Afterwards, error compensation is introduced at necessary locations determined by reinforcement learning to rescue the feature maps with remaining errors. Experimental results demonstrate that inference accuracy of neural networks can be recovered from as low as 1.69% under variations and noise back to more than 95% of their original accuracy, while the training and hardware cost are negligible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge