Correcting discount-factor mismatch in on-policy policy gradient methods
Paper and Code
Jun 23, 2023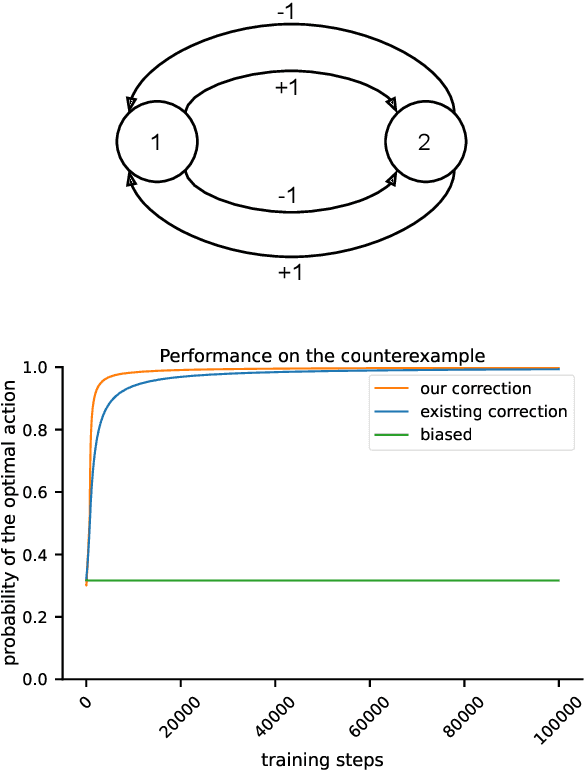
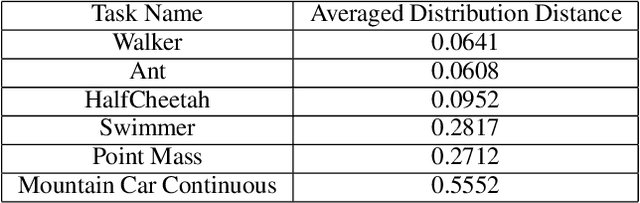
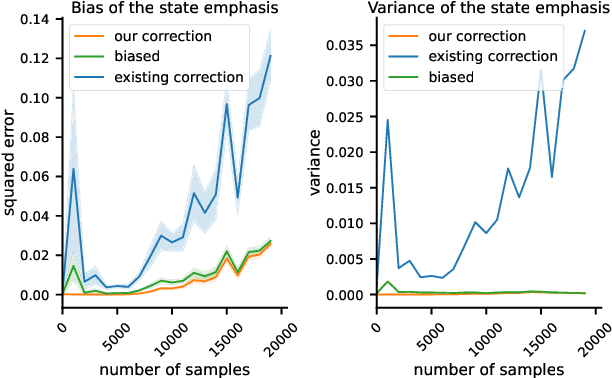
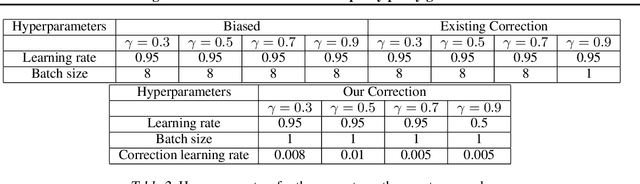
The policy gradient theorem gives a convenient form of the policy gradient in terms of three factors: an action value, a gradient of the action likelihood, and a state distribution involving discounting called the \emph{discounted stationary distribution}. But commonly used on-policy methods based on the policy gradient theorem ignores the discount factor in the state distribution, which is technically incorrect and may even cause degenerate learning behavior in some environments. An existing solution corrects this discrepancy by using $\gamma^t$ as a factor in the gradient estimate. However, this solution is not widely adopted and does not work well in tasks where the later states are similar to earlier states. We introduce a novel distribution correction to account for the discounted stationary distribution that can be plugged into many existing gradient estimators. Our correction circumvents the performance degradation associated with the $\gamma^t$ correction with a lower variance. Importantly, compared to the uncorrected estimators, our algorithm provides improved state emphasis to evade suboptimal policies in certain environments and consistently matches or exceeds the original performance on several OpenAI gym and DeepMind suite benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge