Corralling Stochastic Bandit Algorithms

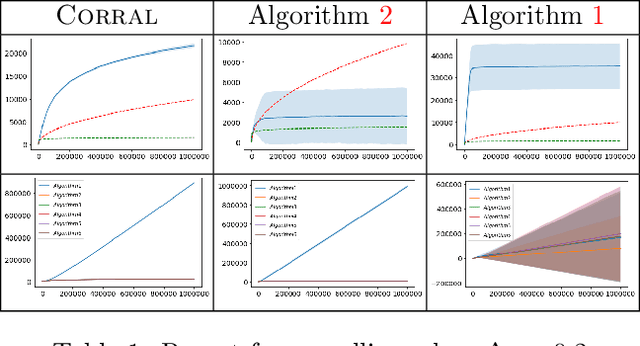
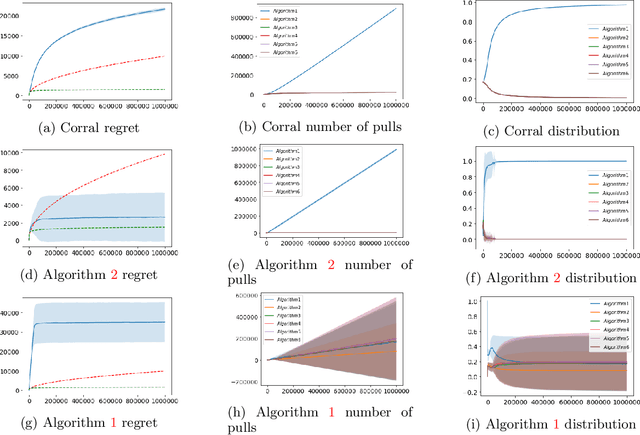
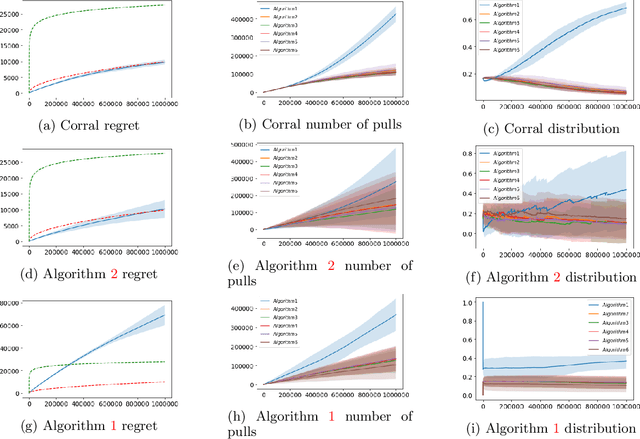
We study the problem of corralling stochastic bandit algorithms, that is combining multiple bandit algorithms designed for a stochastic environment, with the goal of devising a corralling algorithm that performs almost as well as the best base algorithm. We give two general algorithms for this setting, which we show benefit from favorable regret guarantees. We show that the regret of the corralling algorithms is no worse than that of the best algorithm containing the arm with the highest reward, and depends on the gap between the highest reward and other rewards. We also provide lower bounds for this problem that further justify our approach.