Coresets for Vector Summarization with Applications to Network Graphs
Paper and Code
Jun 17, 2017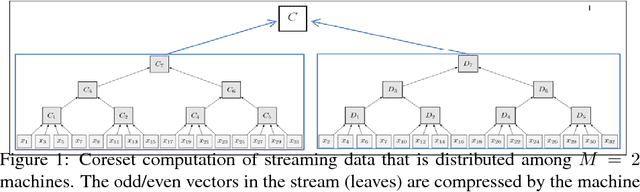
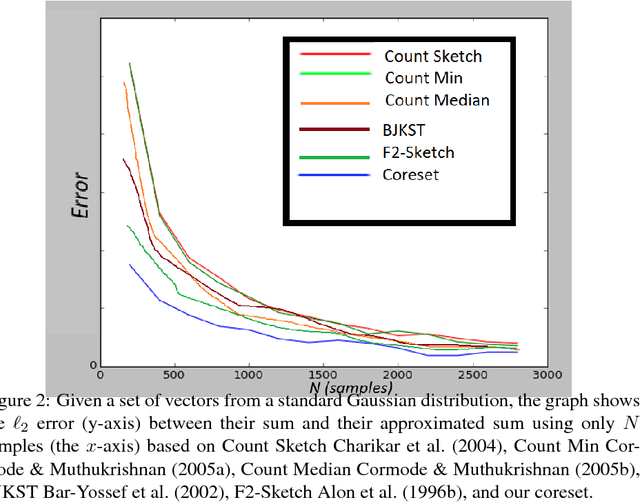
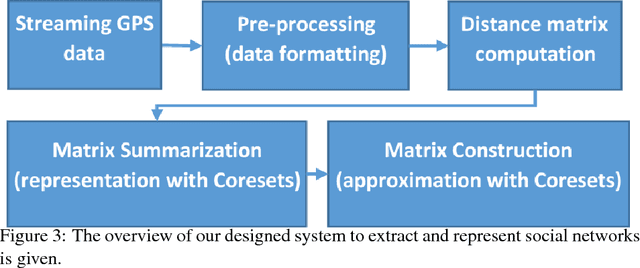
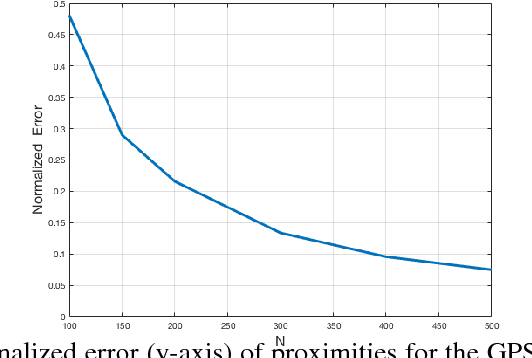
We provide a deterministic data summarization algorithm that approximates the mean $\bar{p}=\frac{1}{n}\sum_{p\in P} p$ of a set $P$ of $n$ vectors in $\REAL^d$, by a weighted mean $\tilde{p}$ of a \emph{subset} of $O(1/\eps)$ vectors, i.e., independent of both $n$ and $d$. We prove that the squared Euclidean distance between $\bar{p}$ and $\tilde{p}$ is at most $\eps$ multiplied by the variance of $P$. We use this algorithm to maintain an approximated sum of vectors from an unbounded stream, using memory that is independent of $d$, and logarithmic in the $n$ vectors seen so far. Our main application is to extract and represent in a compact way friend groups and activity summaries of users from underlying data exchanges. For example, in the case of mobile networks, we can use GPS traces to identify meetings, in the case of social networks, we can use information exchange to identify friend groups. Our algorithm provably identifies the {\it Heavy Hitter} entries in a proximity (adjacency) matrix. The Heavy Hitters can be used to extract and represent in a compact way friend groups and activity summaries of users from underlying data exchanges. We evaluate the algorithm on several large data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge