Coresets for Triangulation
Paper and Code
Jul 18, 2017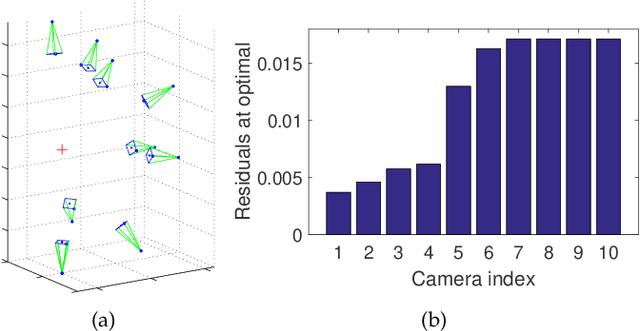

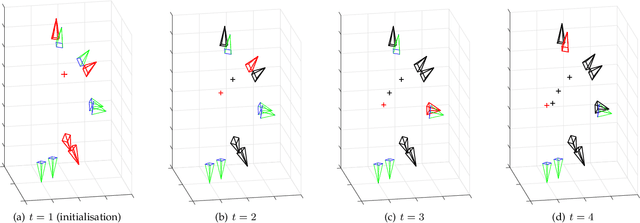

Multiple-view triangulation by $\ell_{\infty}$ minimisation has become established in computer vision. State-of-the-art $\ell_{\infty}$ triangulation algorithms exploit the quasiconvexity of the cost function to derive iterative update rules that deliver the global minimum. Such algorithms, however, can be computationally costly for large problem instances that contain many image measurements, e.g., from web-based photo sharing sites or long-term video recordings. In this paper, we prove that $\ell_{\infty}$ triangulation admits a coreset approximation scheme, which seeks small representative subsets of the input data called coresets. A coreset possesses the special property that the error of the $\ell_{\infty}$ solution on the coreset is within known bounds from the global minimum. We establish the necessary mathematical underpinnings of the coreset algorithm, specifically, by enacting the stopping criterion of the algorithm and proving that the resulting coreset gives the desired approximation accuracy. On large-scale triangulation problems, our method provides theoretically sound approximate solutions. Iterated until convergence, our coreset algorithm is also guaranteed to reach the true optimum. On practical datasets, we show that our technique can in fact attain the global minimiser much faster than current methods
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge