Copula-based mixture model identification for subgroup clustering with imaging applications

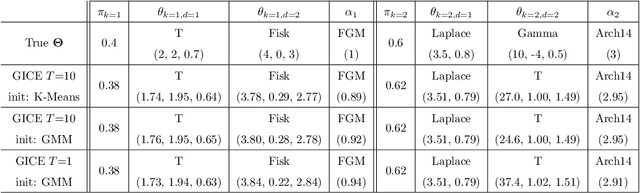
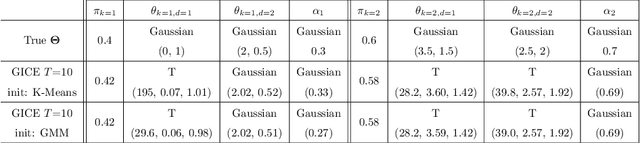
Model-based clustering techniques have been widely applied to various application areas, while most studies focus on canonical mixtures with unique component distribution form. However, this strict assumption is often hard to satisfy. In this paper, we consider the more flexible Copula-Based Mixture Models (CBMMs) for clustering, which allow heterogeneous component distributions composed by flexible choices of marginal and copula forms. More specifically, we propose an adaptation of the Generalized Iterative Conditional Estimation (GICE) algorithm to identify the CBMMs in an unsupervised manner, where the marginal and copula forms and their parameters are estimated iteratively. GICE is adapted from its original version developed for switching Markov model identification with the choice of realization time. Our CBMM-GICE clustering method is then tested on synthetic two-cluster data (N=2000 samples) with discussion of the factors impacting its convergence. Finally, it is compared to the Expectation Maximization identified mixture models with unique component form on the entire MNIST database (N=70000), and on real cardiac magnetic resonance data (N=276) to illustrate its value for imaging applications.