Convolutional Neural Networks combined with Runge-Kutta Methods
Paper and Code
May 19, 2018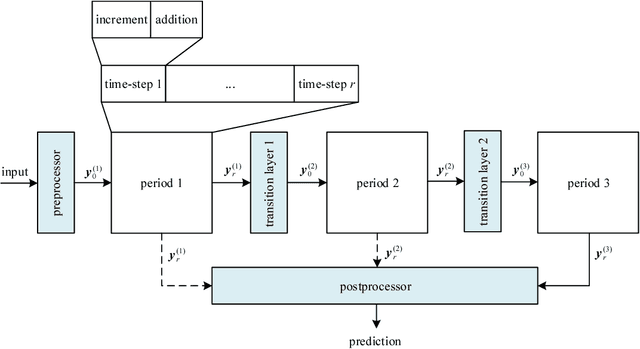

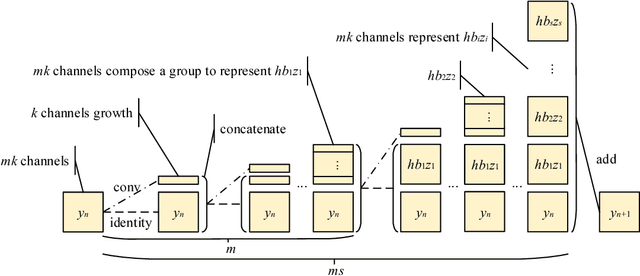
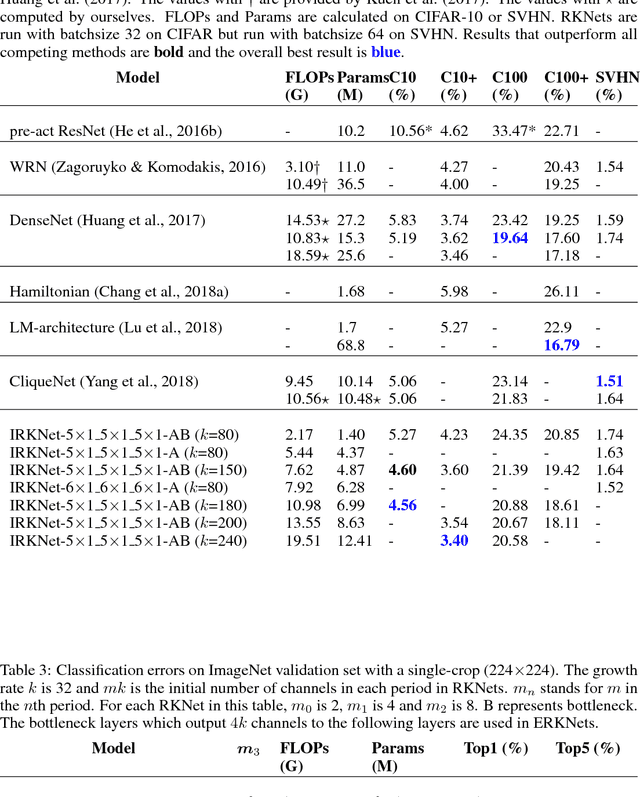
A convolutional neural network for image classification can be constructed mathematically since it is inspired by the ventral stream in visual cortex which can be regarded as a multi-period dynamical system. In this paper, a novel approach is proposed to construct network models from the dynamical systems view. Since a pre-activation residual network can be deemed an approximation of a time-dependent dynamical system using the Euler method, higher order Runge-Kutta methods (RK methods) can be utilized to build network models in order to achieve higher accuracy. The model constructed in such a way is referred to as the Runge-Kutta Convolutional Neural Network (RKNet). RK methods also provide an interpretation of Dense Convolutional Networks (DenseNets) from the dynamical systems view. The proposed methods are evaluated on the benchmark datasets: CIFAR-10/100 and ImageNet. The experimental results show that the RKNets achieve similar accuracy with the state-of-the-art network models, DenseNets. Moreover, the experimental results are consistent with the theoretical properties of RK methods and support the dynamical systems interpretation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge