Convex Shape Representation with Binary Labels for Image Segmentation: Models and Fast Algorithms
Paper and Code
Feb 22, 2020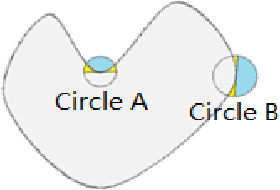

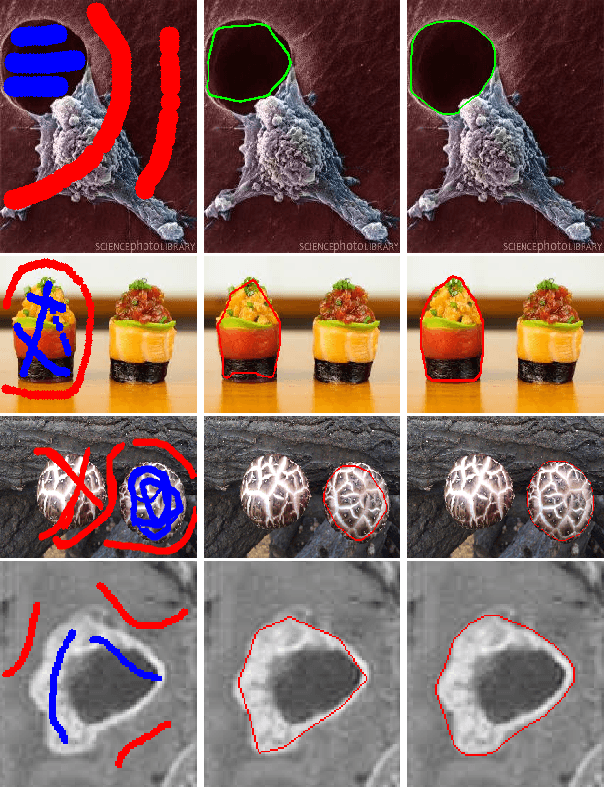

We present a novel and effective binary representation for convex shapes. We show the equivalence between the shape convexity and some properties of the associated indicator function. The proposed method has two advantages. Firstly, the representation is based on a simple inequality constraint on the binary function rather than the definition of convex shapes, which allows us to obtain efficient algorithms for various applications with convexity prior. Secondly, this method is independent of the dimension of the concerned shape. In order to show the effectiveness of the proposed representation approach, we incorporate it with a probability based model for object segmentation with convexity prior. Efficient algorithms are given to solve the proposed models using Lagrange multiplier methods and linear approximations. Various experiments are given to show the superiority of the proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge