Convergence of Parameter Estimates for Regularized Mixed Linear Regression Models
Paper and Code
Mar 21, 2019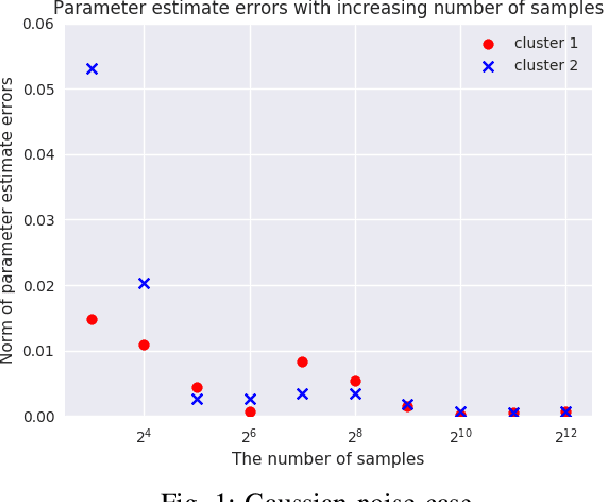
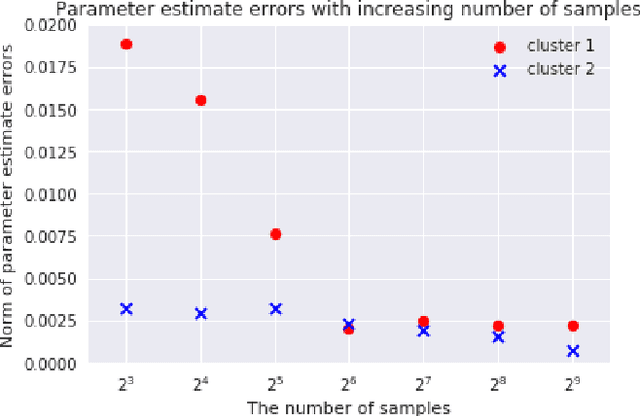
We consider {\em Mixed Linear Regression (MLR)}, where training data have been generated from a mixture of distinct linear models (or clusters) and we seek to identify the corresponding coefficient vectors. We introduce a {\em Mixed Integer Programming (MIP)} formulation for MLR subject to regularization constraints on the coefficient vectors. We establish that as the number of training samples grows large, the MIP solution converges to the true coefficient vectors in the absence of noise. Subject to slightly stronger assumptions, we also establish that the MIP identifies the clusters from which the training samples were generated. In the special case where training data come from a single cluster, we establish that the corresponding MIP yields a solution that converges to the true coefficient vector even when training data are perturbed by (martingale difference) noise. We provide a counterexample indicating that in the presence of noise, the MIP may fail to produce the true coefficient vectors for more than one clusters. We also provide numerical results testing the MIP solutions in synthetic examples with noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge