Convergence Analysis of Batch Normalization for Deep Neural Nets

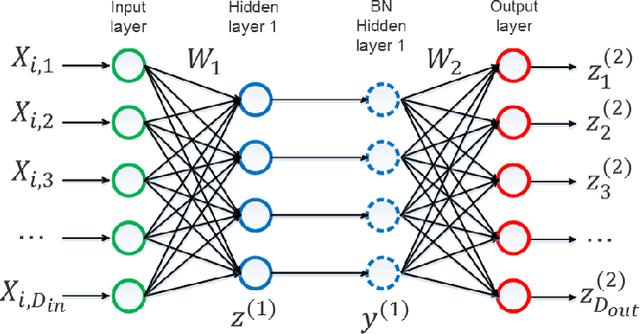
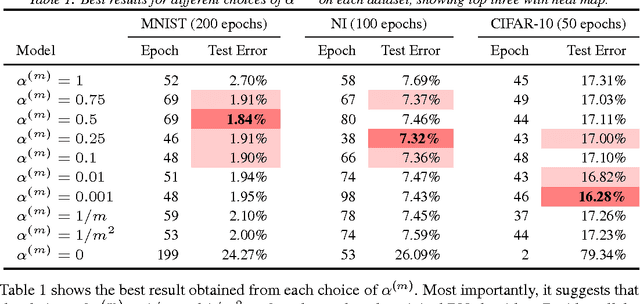
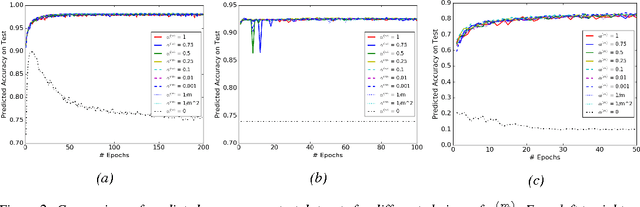
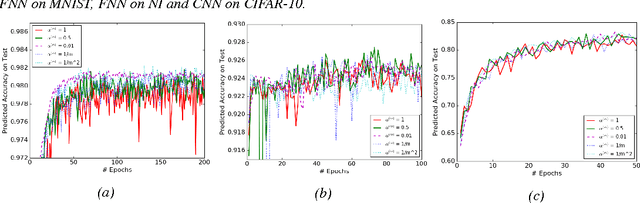
Batch normalization (BN) is very effective in accelerating the convergence of a neural network training phase that it has become a common practice. We propose a generalization of BN, the diminishing batch normalization (DBN) algorithm. We provide an analysis of the convergence of the DBN algorithm that converges to a stationary point with respect to trainable parameters. We analyze a two layer model with linear activation. The main challenge of the analysis is the fact that some parameters are updated by gradient while others are not. In the numerical experiments, we use models with more layers and ReLU activation. We observe that DBN outperforms the original BN algorithm on MNIST, NI and CIFAR-10 datasets with reasonable complex FNN and CNN models.