Convergence Analyses of Online ADAM Algorithm in Convex Setting and Two-Layer ReLU Neural Network
Paper and Code
May 22, 2019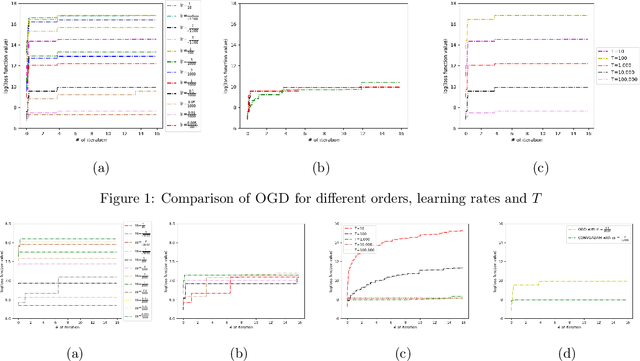

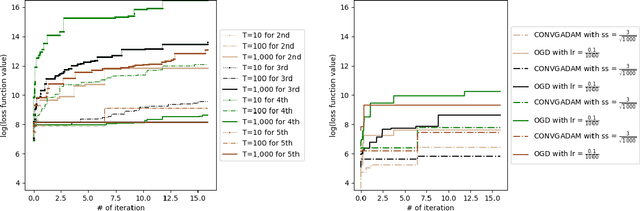
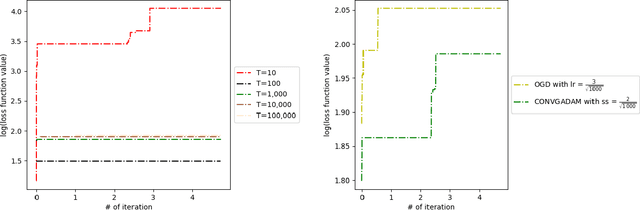
Nowadays, online learning is an appealing learning paradigm, which is of great interest in practice due to the recent emergence of large scale applications such as online advertising placement and online web ranking. Standard online learning assumes a finite number of samples while in practice data is streamed infinitely. In such a setting gradient descent with a diminishing learning rate does not work. We first introduce regret with rolling window, a new performance metric for online streaming learning, which measures the performance of an algorithm on every fixed number of contiguous samples. At the same time, we propose a family of algorithms based on gradient descent with a constant or adaptive learning rate and provide very technical analyses establishing regret bound properties of the algorithms. We cover the convex setting showing the regret of the order of the square root of the size of the window in the constant and dynamic learning rate scenarios. Our proof is applicable also to the standard online setting where we provide the first analysis of the same regret order (the previous proofs have flaws). We also study a two layer neural network setting with ReLU activation. In this case we establish that if initial weights are close to a stationary point, the same square root regret bound is attainable. We conduct computational experiments demonstrating a superior performance of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge