Controlling the False Split Rate in Tree-Based Aggregation
Paper and Code
Aug 11, 2021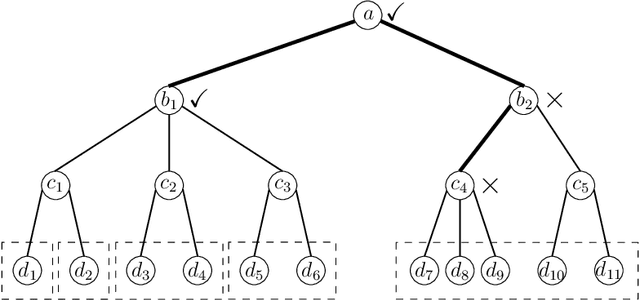
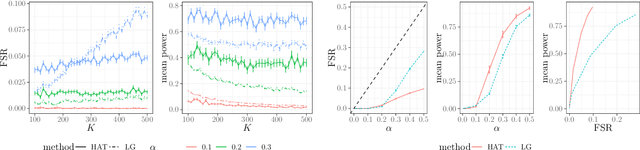
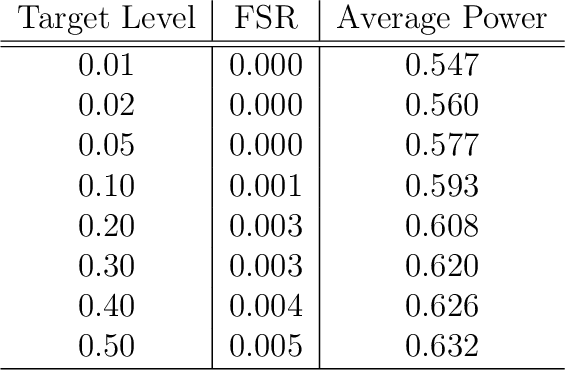
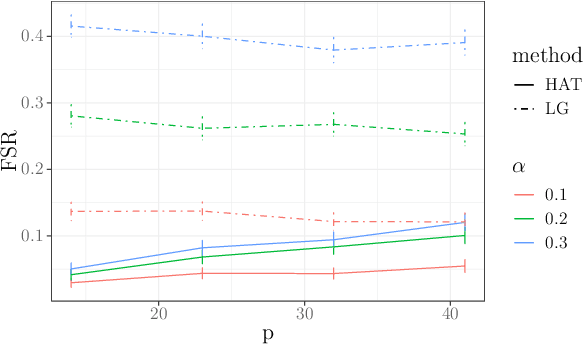
In many domains, data measurements can naturally be associated with the leaves of a tree, expressing the relationships among these measurements. For example, companies belong to industries, which in turn belong to ever coarser divisions such as sectors; microbes are commonly arranged in a taxonomic hierarchy from species to kingdoms; street blocks belong to neighborhoods, which in turn belong to larger-scale regions. The problem of tree-based aggregation that we consider in this paper asks which of these tree-defined subgroups of leaves should really be treated as a single entity and which of these entities should be distinguished from each other. We introduce the "false split rate", an error measure that describes the degree to which subgroups have been split when they should not have been. We then propose a multiple hypothesis testing algorithm for tree-based aggregation, which we prove controls this error measure. We focus on two main examples of tree-based aggregation, one which involves aggregating means and the other which involves aggregating regression coefficients. We apply this methodology to aggregate stocks based on their volatility and to aggregate neighborhoods of New York City based on taxi fares.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge