Control with adaptive Q-learning
Paper and Code
Nov 03, 2020
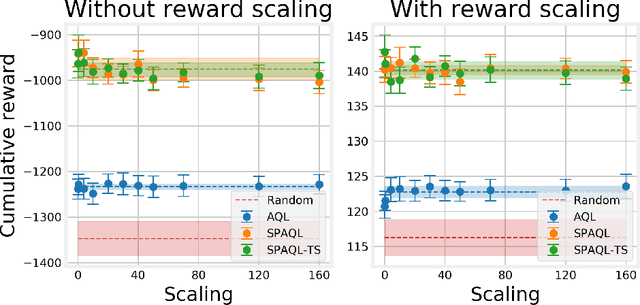

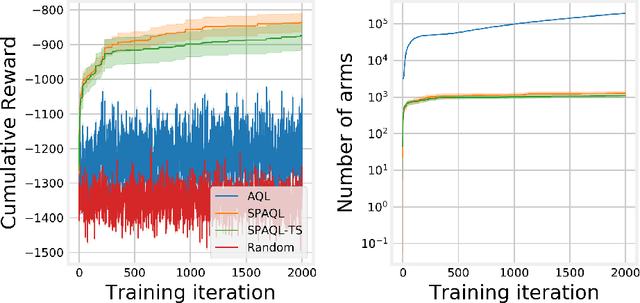
This paper evaluates adaptive Q-learning (AQL) and single-partition adaptive Q-learning (SPAQL), two algorithms for efficient model-free episodic reinforcement learning (RL), in two classical control problems (Pendulum and Cartpole). AQL adaptively partitions the state-action space of a Markov decision process (MDP), while learning the control policy, i. e., the mapping from states to actions. The main difference between AQL and SPAQL is that the latter learns time-invariant policies, where the mapping from states to actions does not depend explicitly on the time step. This paper also proposes the SPAQL with terminal state (SPAQL-TS), an improved version of SPAQL tailored for the design of regulators for control problems. The time-invariant policies are shown to result in a better performance than the time-variant ones in both problems studied. These algorithms are particularly fitted to RL problems where the action space is finite, as is the case with the Cartpole problem. SPAQL-TS solves the OpenAI Gym Cartpole problem, while also displaying a higher sample efficiency than trust region policy optimization (TRPO), a standard RL algorithm for solving control tasks. Moreover, the policies learned by SPAQL are interpretable, while TRPO policies are typically encoded as neural networks, and therefore hard to interpret. Yielding interpretable policies while being sample-efficient are the major advantages of SPAQL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge