Contrastive Bayesian Analysis for Deep Metric Learning
Paper and Code
Oct 10, 2022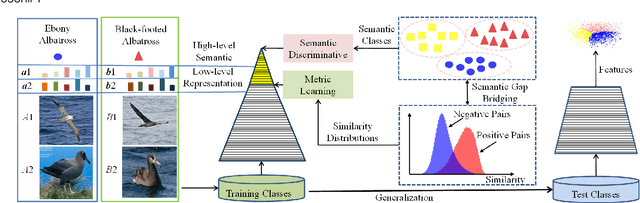
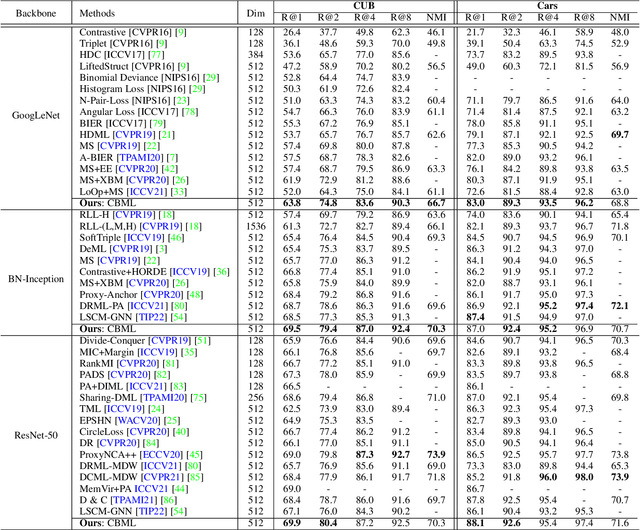
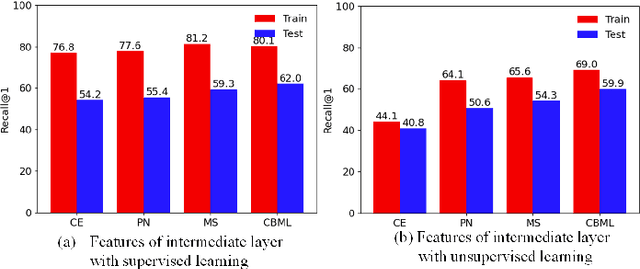
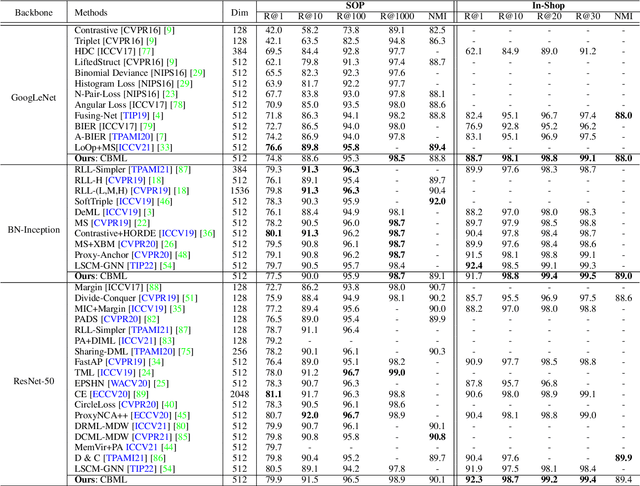
Recent methods for deep metric learning have been focusing on designing different contrastive loss functions between positive and negative pairs of samples so that the learned feature embedding is able to pull positive samples of the same class closer and push negative samples from different classes away from each other. In this work, we recognize that there is a significant semantic gap between features at the intermediate feature layer and class labels at the final output layer. To bridge this gap, we develop a contrastive Bayesian analysis to characterize and model the posterior probabilities of image labels conditioned by their features similarity in a contrastive learning setting. This contrastive Bayesian analysis leads to a new loss function for deep metric learning. To improve the generalization capability of the proposed method onto new classes, we further extend the contrastive Bayesian loss with a metric variance constraint. Our experimental results and ablation studies demonstrate that the proposed contrastive Bayesian metric learning method significantly improves the performance of deep metric learning in both supervised and pseudo-supervised scenarios, outperforming existing methods by a large margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge