Continual learning with direction-constrained optimization
Paper and Code
Nov 25, 2020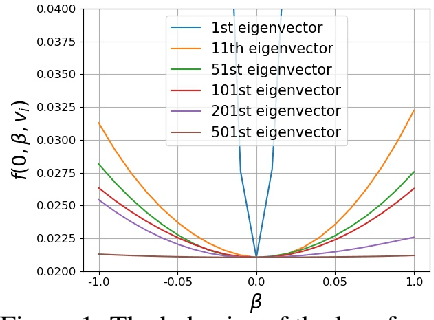
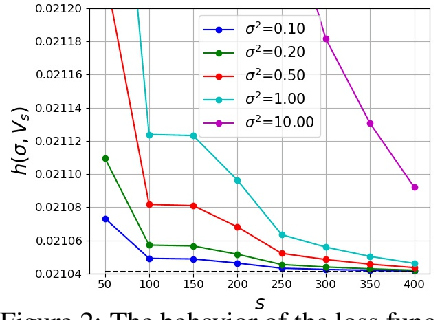
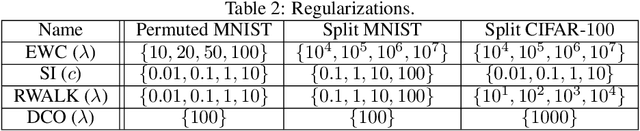
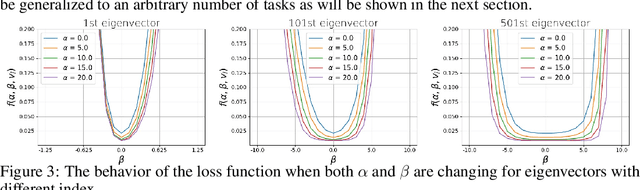
This paper studies a new design of the optimization algorithm for training deep learning models with a fixed architecture of the classification network in a continual learning framework, where the training data is non-stationary and the non-stationarity is imposed by a sequence of distinct tasks. This setting implies the existence of a manifold of network parameters that correspond to good performance of the network on all tasks. Our algorithm is derived from the geometrical properties of this manifold. We first analyze a deep model trained on only one learning task in isolation and identify a region in network parameter space, where the model performance is close to the recovered optimum. We provide empirical evidence that this region resembles a cone that expands along the convergence direction. We study the principal directions of the trajectory of the optimizer after convergence and show that traveling along a few top principal directions can quickly bring the parameters outside the cone but this is not the case for the remaining directions. We argue that catastrophic forgetting in a continual learning setting can be alleviated when the parameters are constrained to stay within the intersection of the plausible cones of individual tasks that were so far encountered during training. Enforcing this is equivalent to preventing the parameters from moving along the top principal directions of convergence corresponding to the past tasks. For each task we introduce a new linear autoencoder to approximate its corresponding top forbidden principal directions. They are then incorporated into the loss function in the form of a regularization term for the purpose of learning the coming tasks without forgetting. We empirically demonstrate that our algorithm performs favorably compared to other state-of-art regularization-based continual learning methods, including EWC and SI.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge