Contact-Aided Invariant Extended Kalman Filtering for Legged Robot State Estimation
Paper and Code
May 26, 2018

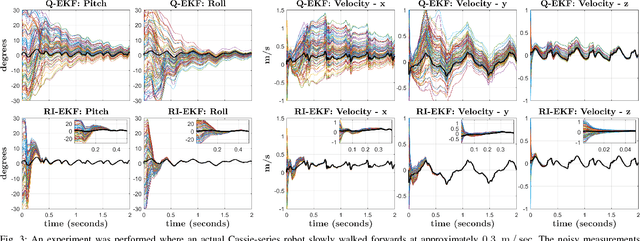
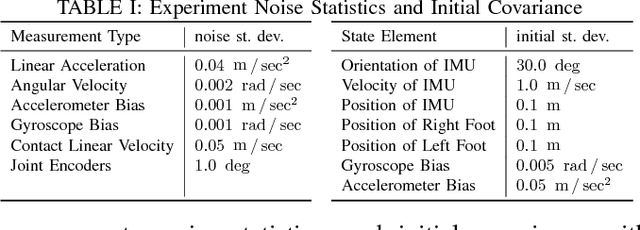
This paper derives a contact-aided inertial navigation observer for a 3D bipedal robot using the theory of invariant observer design. Aided inertial navigation is fundamentally a nonlinear observer design problem; thus, current solutions are based on approximations of the system dynamics, such as an Extended Kalman Filter (EKF), which uses a system's Jacobian linearization along the current best estimate of its trajectory. On the basis of the theory of invariant observer design by Barrau and Bonnabel, and in particular, the Invariant EKF (InEKF), we show that the error dynamics of the point contact-inertial system follows a log-linear autonomous differential equation; hence, the observable state variables can be rendered convergent with a domain of attraction that is independent of the system's trajectory. Due to the log-linear form of the error dynamics, it is not necessary to perform a nonlinear observability analysis to show that when using an Inertial Measurement Unit (IMU) and contact sensors, the absolute position of the robot and a rotation about the gravity vector (yaw) are unobservable. We further augment the state of the developed InEKF with IMU biases, as the online estimation of these parameters has a crucial impact on system performance. We evaluate the convergence of the proposed system with the commonly used quaternion-based EKF observer using a Monte-Carlo simulation. In addition, our experimental evaluation using a Cassie-series bipedal robot shows that the contact-aided InEKF provides better performance in comparison with the quaternion-based EKF as a result of exploiting symmetries present in the system dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge