Constraints on Hebbian and STDP learned weights of a spiking neuron
Paper and Code
Dec 14, 2020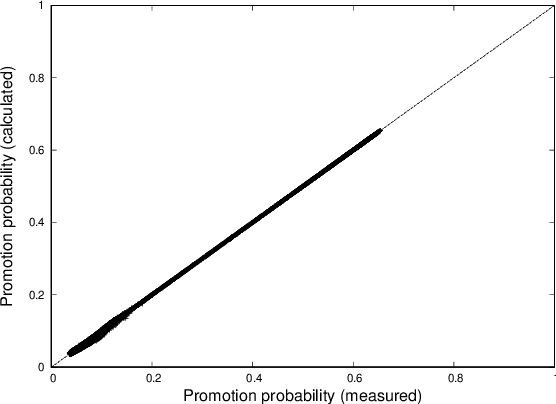
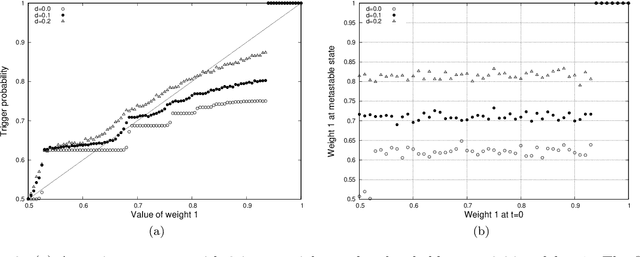
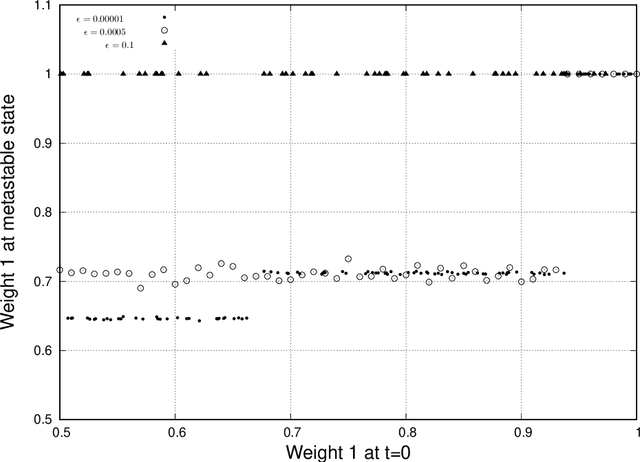
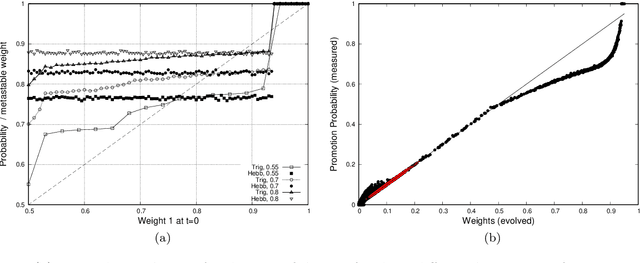
We analyse mathematically the constraints on weights resulting from Hebbian and STDP learning rules applied to a spiking neuron with weight normalisation. In the case of pure Hebbian learning, we find that the normalised weights equal the promotion probabilities of weights up to correction terms that depend on the learning rate and are usually small. A similar relation can be derived for STDP algorithms, where the normalised weight values reflect a difference between the promotion and demotion probabilities of the weight. These relations are practically useful in that they allow checking for convergence of Hebbian and STDP algorithms. Another application is novelty detection. We demonstrate this using the MNIST dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge