Constrained Upper Confidence Reinforcement Learning
Paper and Code
Jan 26, 2020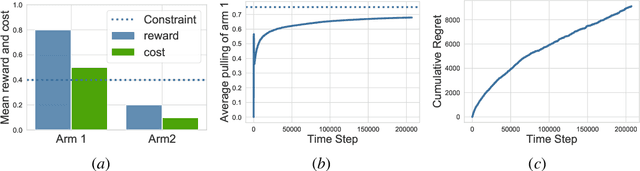
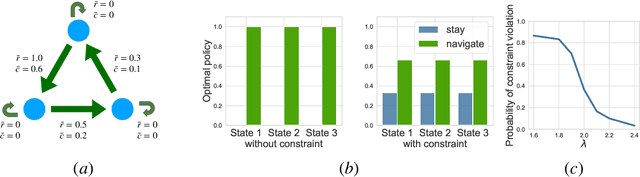
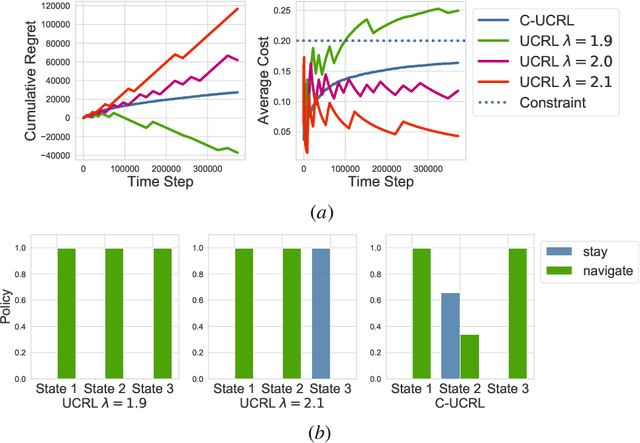
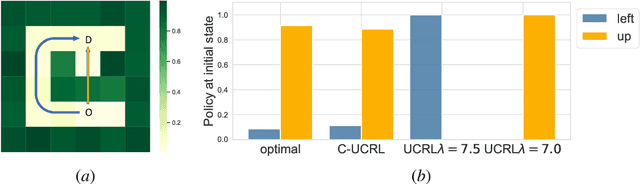
Constrained Markov Decision Processes are a class of stochastic decision problems in which the decision maker must select a policy that satisfies auxiliary cost constraints. This paper extends upper confidence reinforcement learning for settings in which the reward function and the constraints, described by cost functions, are unknown a priori but the transition kernel is known. Such a setting is well-motivated by a number of applications including exploration of unknown, potentially unsafe, environments. We present an algorithm C-UCRL and show that it achieves sub-linear regret ($ O(T^{\frac{3}{4}}\sqrt{\log(T/\delta)})$) with respect to the reward while satisfying the constraints even while learning with probability $1-\delta$. Illustrative examples are provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge