Constrained Overcomplete Analysis Operator Learning for Cosparse Signal Modelling
Paper and Code
Feb 20, 2013

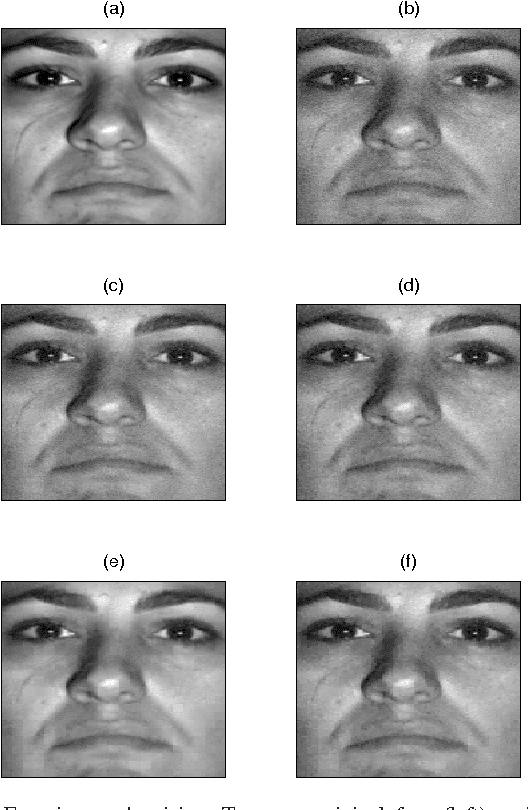
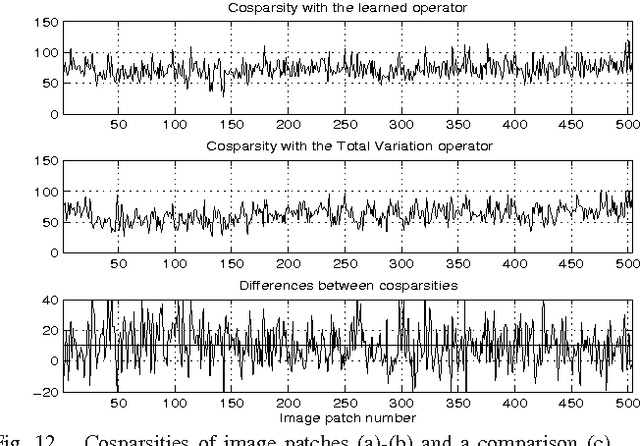
We consider the problem of learning a low-dimensional signal model from a collection of training samples. The mainstream approach would be to learn an overcomplete dictionary to provide good approximations of the training samples using sparse synthesis coefficients. This famous sparse model has a less well known counterpart, in analysis form, called the cosparse analysis model. In this new model, signals are characterised by their parsimony in a transformed domain using an overcomplete (linear) analysis operator. We propose to learn an analysis operator from a training corpus using a constrained optimisation framework based on L1 optimisation. The reason for introducing a constraint in the optimisation framework is to exclude trivial solutions. Although there is no final answer here for which constraint is the most relevant constraint, we investigate some conventional constraints in the model adaptation field and use the uniformly normalised tight frame (UNTF) for this purpose. We then derive a practical learning algorithm, based on projected subgradients and Douglas-Rachford splitting technique, and demonstrate its ability to robustly recover a ground truth analysis operator, when provided with a clean training set, of sufficient size. We also find an analysis operator for images, using some noisy cosparse signals, which is indeed a more realistic experiment. As the derived optimisation problem is not a convex program, we often find a local minimum using such variational methods. Some local optimality conditions are derived for two different settings, providing preliminary theoretical support for the well-posedness of the learning problem under appropriate conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge