Constant matters: Fine-grained Complexity of Differentially Private Continual Observation
Paper and Code
Apr 04, 2022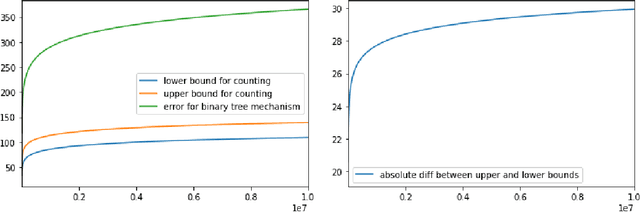
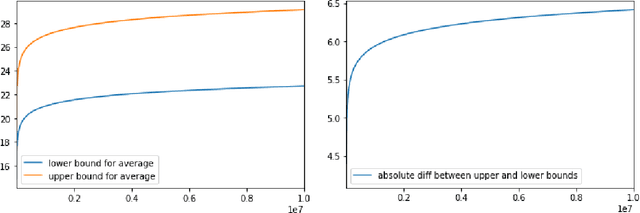
We study fine-grained error bounds for differentially private algorithms for averaging and counting under continual observation. Our main insight is that the factorization mechanism when using lower-triangular matrices, can be used in the continual observation model. We give explicit factorizations for two fundamental matrices, namely the counting matrix $M_{\mathsf{count}}$ and the averaging matrix $M_{\mathsf{average}}$ and show fine-grained bounds for the additive error of the resulting mechanism using the {\em completely bounded norm} (cb-norm) or {\em factorization norm}. Our bound on the cb-norm for $M_{\mathsf{count}}$ is tight up an additive error of 1 and the bound for $M_{\mathsf{average}}$ is tight up to $\approx 0.64$. This allows us to give the first algorithm for averaging whose additive error has $o(\log^{3/2} T)$ dependence. Furthermore, we are the first to give concrete error bounds for various problems under continual observation such as binary counting, maintaining a histogram, releasing an approximately cut-preserving synthetic graph, many graph-based statistics, and substring and episode counting. Finally, we present a fine-grained error bound for non-interactive local learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge