Conservative Stochastic Optimization with Expectation Constraints

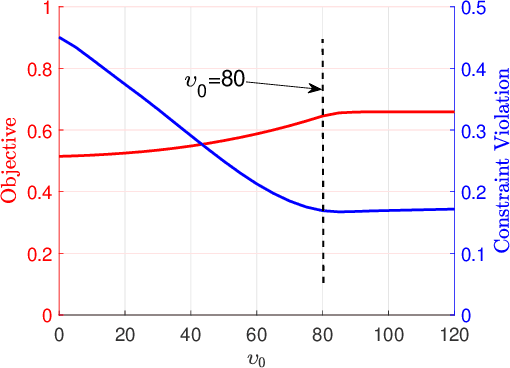
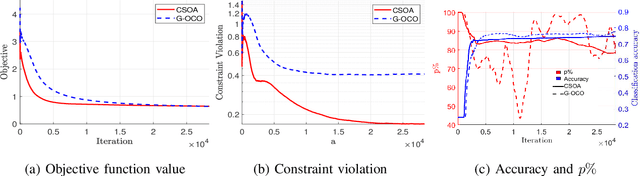
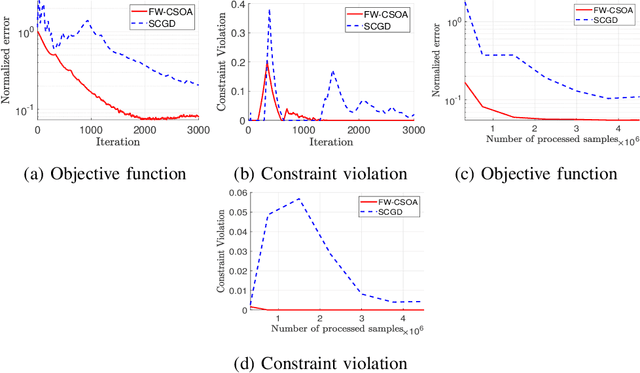
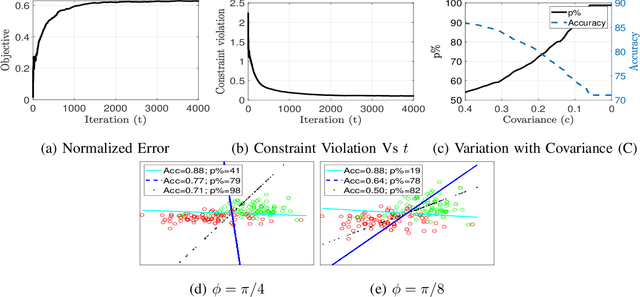
This paper considers stochastic convex optimization problems where the objective and constraint functions involve expectations with respect to the data indices or environmental variables, in addition to deterministic convex constraints on the domain of the variables. Although the setting is generic and arises in different machine learning applications, online and efficient approaches for solving such problems have not been widely studied. Since the underlying data distribution is unknown a priori, a closed-form solution is generally not available, and classical deterministic optimization paradigms are not applicable. State-of-the-art approaches, such as those using the saddle point framework, can ensure that the optimality gap as well as the constraint violation decay as $\O\left(T^{-\frac{1}{2}}\right)$ where $T$ is the number of stochastic gradients. The domain constraints are assumed simple and handled via projection at every iteration. In this work, we propose a novel conservative stochastic optimization algorithm (CSOA) that achieves zero constraint violation and $\O\left(T^{-\frac{1}{2}}\right)$ optimality gap. Further, the projection operation (for scenarios when calculating projection is expensive) in the proposed algorithm can be avoided by considering the conditional gradient or Frank-Wolfe (FW) variant of the algorithm. The state-of-the-art stochastic FW variants achieve an optimality gap of $\O\left(T^{-\frac{1}{3}}\right)$ after $T$ iterations, though these algorithms have not been applied to problems with functional expectation constraints. In this work, we propose the FW-CSOA algorithm that is not only projection-free but also achieves zero constraint violation with $\O\left(T^{-\frac{1}{4}}\right)$ decay of the optimality gap. The efficacy of the proposed algorithms is tested on two relevant problems: fair classification and structured matrix completion.