Consensus-Based Modelling using Distributed Feature Construction
Paper and Code
Sep 11, 2014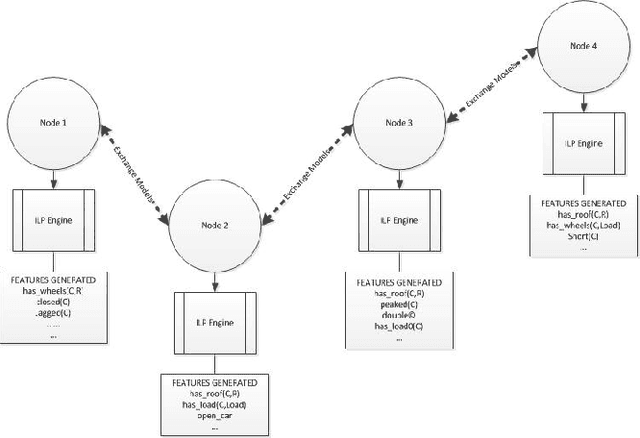
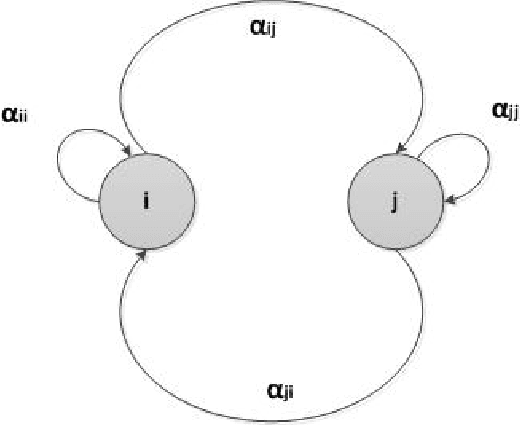
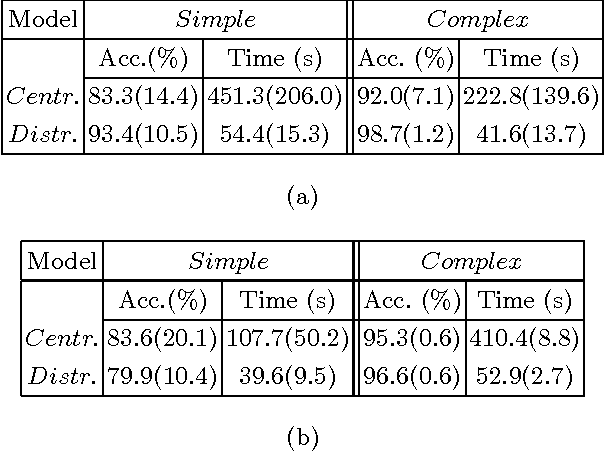
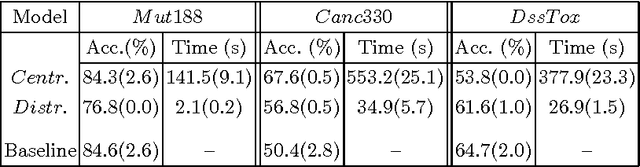
A particularly successful role for Inductive Logic Programming (ILP) is as a tool for discovering useful relational features for subsequent use in a predictive model. Conceptually, the case for using ILP to construct relational features rests on treating these features as functions, the automated discovery of which necessarily requires some form of first-order learning. Practically, there are now several reports in the literature that suggest that augmenting any existing features with ILP-discovered relational features can substantially improve the predictive power of a model. While the approach is straightforward enough, much still needs to be done to scale it up to explore more fully the space of possible features that can be constructed by an ILP system. This is in principle, infinite and in practice, extremely large. Applications have been confined to heuristic or random selections from this space. In this paper, we address this computational difficulty by allowing features to be constructed in a distributed manner. That is, there is a network of computational units, each of which employs an ILP engine to construct some small number of features and then builds a (local) model. We then employ a consensus-based algorithm, in which neighboring nodes share information to update local models. For a category of models (those with convex loss functions), it can be shown that the algorithm will result in all nodes converging to a consensus model. In practice, it may be slow to achieve this convergence. Nevertheless, our results on synthetic and real datasets that suggests that in relatively short time the "best" node in the network reaches a model whose predictive accuracy is comparable to that obtained using more computational effort in a non-distributed setting (the best node is identified as the one whose weights converge first).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge