Conformalized Online Learning: Online Calibration Without a Holdout Set
Paper and Code
May 19, 2022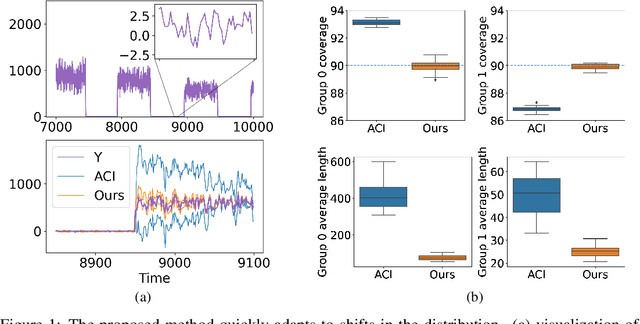

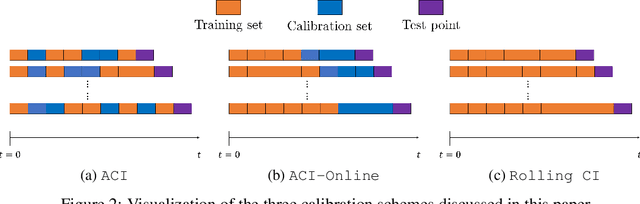
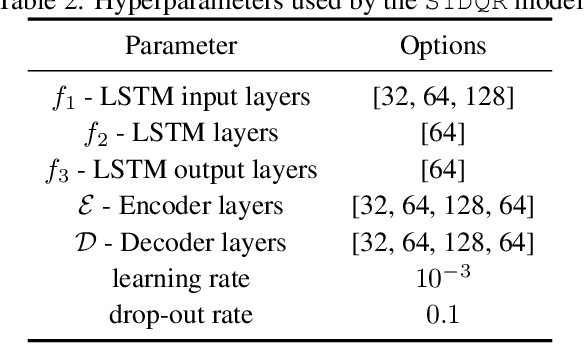
We develop a framework for constructing uncertainty sets with a valid coverage guarantee in an online setting, in which the underlying data distribution can drastically -- and even adversarially -- shift over time. The technique we propose is highly flexible as it can be integrated with any online learning algorithm, requiring minimal implementation effort and computational cost. A key advantage of our method over existing alternatives -- which also build on conformal inference -- is that we do not need to split the data into training and holdout calibration sets. This allows us to fit the predictive model in a fully online manner, utilizing the most recent observation for constructing calibrated uncertainty sets. Consequently, and in contrast with existing techniques, (i) the sets we build can quickly adapt to new changes in the distribution; and (ii) our procedure does not require refitting the model at each time step. Using synthetic and real-world benchmark data sets, we demonstrate the validity of our theory and the improved performance of our proposal over existing techniques. To demonstrate the greater flexibility of the proposed method, we show how to construct valid intervals for a multiple-output regression problem that previous sequential calibration methods cannot handle due to impractical computational and memory requirements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge