Conformalized Link Prediction on Graph Neural Networks
Paper and Code
Jun 26, 2024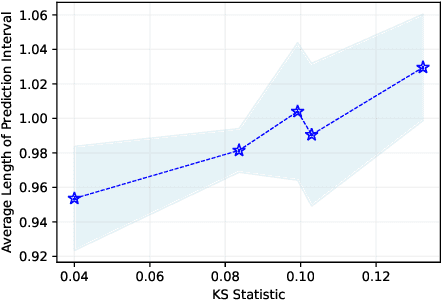
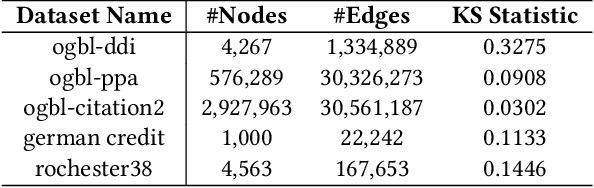
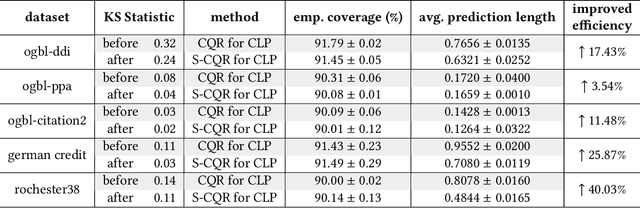
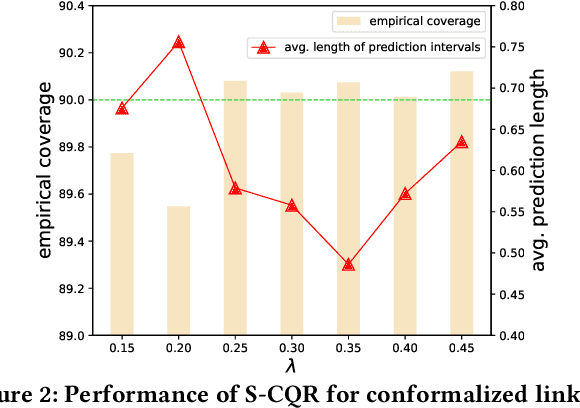
Graph Neural Networks (GNNs) excel in diverse tasks, yet their applications in high-stakes domains are often hampered by unreliable predictions. Although numerous uncertainty quantification methods have been proposed to address this limitation, they often lack \textit{rigorous} uncertainty estimates. This work makes the first attempt to introduce a distribution-free and model-agnostic uncertainty quantification approach to construct a predictive interval with a statistical guarantee for GNN-based link prediction. We term it as \textit{conformalized link prediction.} Our approach builds upon conformal prediction (CP), a framework that promises to construct statistically robust prediction sets or intervals. We first theoretically and empirically establish a permutation invariance condition for the application of CP in link prediction tasks, along with an exact test-time coverage. Leveraging the important structural information in graphs, we then identify a novel and crucial connection between a graph's adherence to the power law distribution and the efficiency of CP. This insight leads to the development of a simple yet effective sampling-based method to align the graph structure with a power law distribution prior to the standard CP procedure. Extensive experiments demonstrate that for conformalized link prediction, our approach achieves the desired marginal coverage while significantly improving the efficiency of CP compared to baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge