Computing Posterior Probabilities of Structural Features in Bayesian Networks
Paper and Code
May 09, 2012
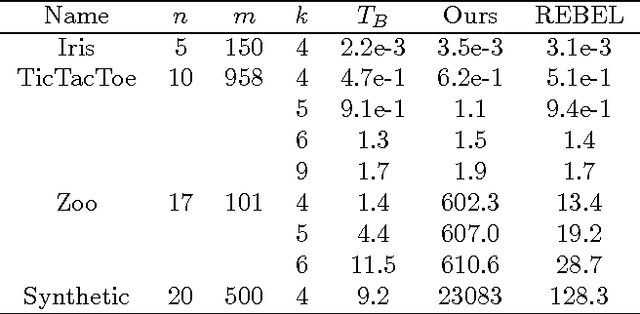


We study the problem of learning Bayesian network structures from data. Koivisto and Sood (2004) and Koivisto (2006) presented algorithms that can compute the exact marginal posterior probability of a subnetwork, e.g., a single edge, in O(n2n) time and the posterior probabilities for all n(n-1) potential edges in O(n2n) total time, assuming that the number of parents per node or the indegree is bounded by a constant. One main drawback of their algorithms is the requirement of a special structure prior that is non uniform and does not respect Markov equivalence. In this paper, we develop an algorithm that can compute the exact posterior probability of a subnetwork in O(3n) time and the posterior probabilities for all n(n-1) potential edges in O(n3n) total time. Our algorithm also assumes a bounded indegree but allows general structure priors. We demonstrate the applicability of the algorithm on several data sets with up to 20 variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge