Computing large market equilibria using abstractions

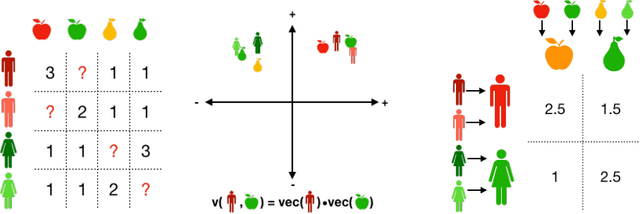
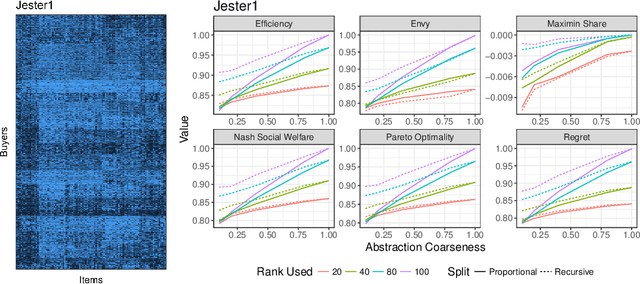
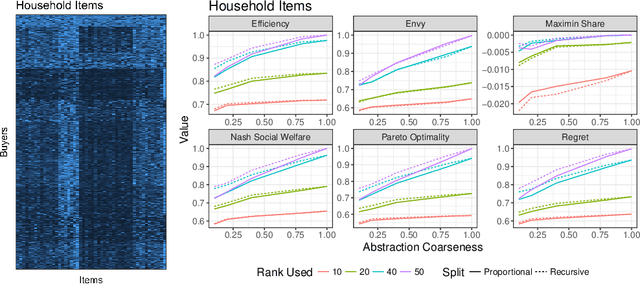
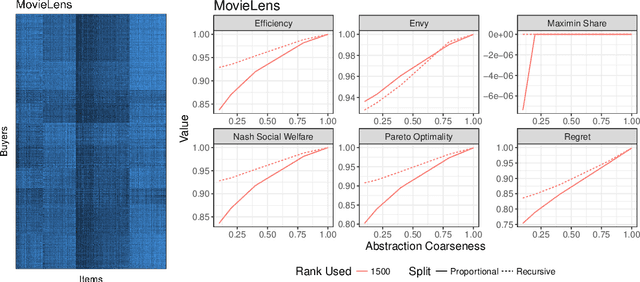
Computing market equilibria is an important practical problem for market design (e.g. fair division, item allocation). However, computing equilibria requires large amounts of information (e.g. all valuations for all buyers for all items) and compute power. We consider ameliorating these issues by applying a method used for solving complex games: constructing a coarsened abstraction of a given market, solving for the equilibrium in the abstraction, and lifting the prices and allocations back to the original market. We show how to bound important quantities such as regret, envy, Nash social welfare, Pareto optimality, and maximin share when the abstracted prices and allocations are used in place of the real equilibrium. We then study two abstraction methods of interest for practitioners: 1) filling in unknown valuations using techniques from matrix completion, 2) reducing the problem size by aggregating groups of buyers/items into smaller numbers of representative buyers/items and solving for equilibrium in this coarsened market. We find that in real data allocations/prices that are relatively close to equilibria can be computed from even very coarse abstractions.