Computing Complexity-aware Plans Using Kolmogorov Complexity
Paper and Code
Sep 22, 2021
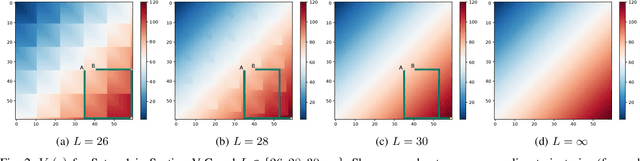
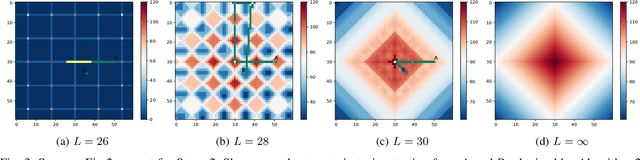

In this paper, we introduce complexity-aware planning for finite-horizon deterministic finite automata with rewards as outputs, based on Kolmogorov complexity. Kolmogorov complexity is considered since it can detect computational regularities of deterministic optimal policies. We present a planning objective yielding an explicit trade-off between a policy's performance and complexity. It is proven that maximising this objective is non-trivial in the sense that dynamic programming is infeasible. We present two algorithms obtaining low-complexity policies, where the first algorithm obtains a low-complexity optimal policy, and the second algorithm finds a policy maximising performance while maintaining local (stage-wise) complexity constraints. We evaluate the algorithms on a simple navigation task for a mobile robot, where our algorithms yield low-complexity policies that concur with intuition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge