Compressive-Sensing Data Reconstruction for Structural Health Monitoring: A Machine-Learning Approach
Paper and Code
Jan 07, 2019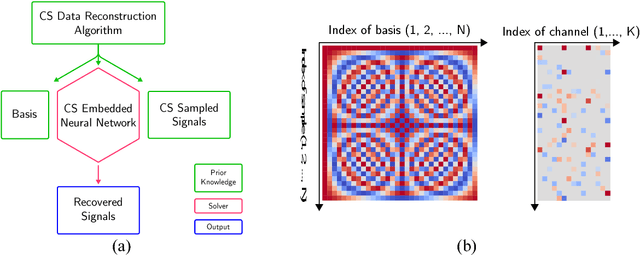
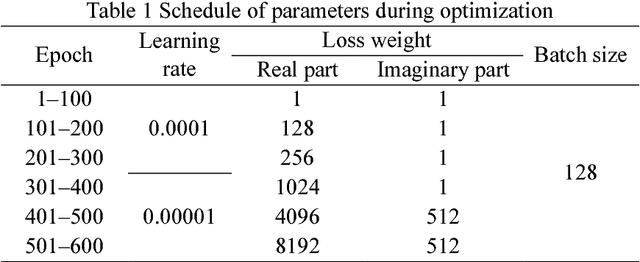
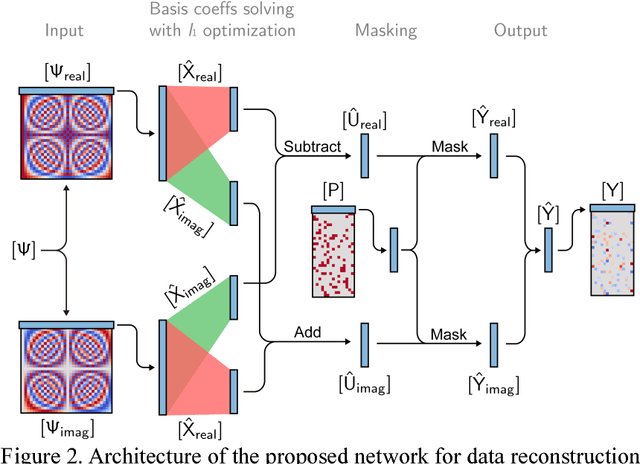
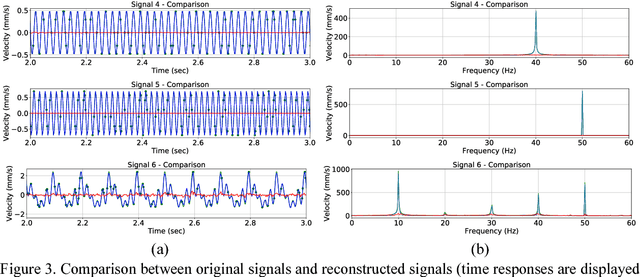
Compressive sensing (CS) has been studied and applied in structural health monitoring for wireless data acquisition and transmission, structural modal identification, and spare damage identification. The key issue in CS is finding the optimal solution for sparse optimization. In the past years, many algorithms have been proposed in the field of applied mathematics. In this paper, we propose a machine-learning-based approach to solve the CS data-reconstruction problem. By treating a computation process as a data flow, the process of CS-based data reconstruction is formalized into a standard supervised-learning task. The prior knowledge, i.e., the basis matrix and the CS-sampled signals, are used as the input and the target of the network; the basis coefficient matrix is embedded as the parameters of a certain layer; the objective function of conventional compressive sensing is set as the loss function of the network. Regularized by l1-norm, these basis coefficients are optimized to reduce the error between the original CS-sampled signals and the masked reconstructed signals with a common optimization algorithm. Also, the proposed network can handle complex bases, such as a Fourier basis. Benefiting from the nature of a multi-neuron layer, multiple signal channels can be reconstructed simultaneously. Meanwhile, the disassembled use of a large-scale basis makes the method memory-efficient. A numerical example of multiple sinusoidal waves and an example of field-test wireless data from a suspension bridge are carried out to illustrate the data-reconstruction ability of the proposed approach. The results show that high reconstruction accuracy can be obtained by the machine learning-based approach. Also, the parameters of the network have clear meanings; the inference of the mapping between input and output is fully transparent, making the CS data reconstruction neural network interpretable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge