Complexity Results and Algorithms for Bipolar Argumentation
Paper and Code
Mar 05, 2019
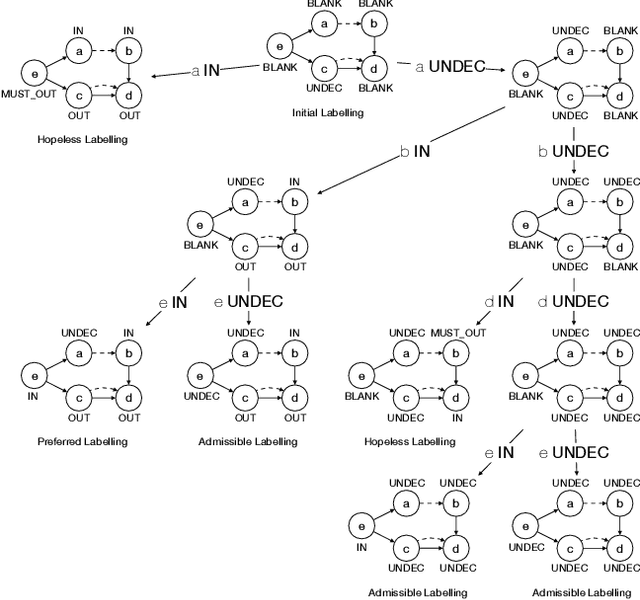

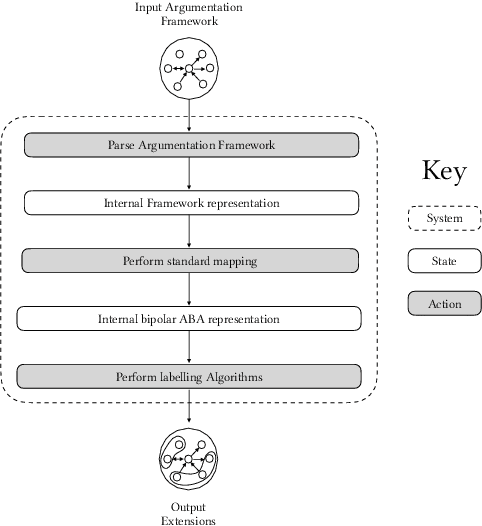
Bipolar Argumentation Frameworks (BAFs) admit several interpretations of the support relation and diverging definitions of semantics. Recently, several classes of BAFs have been captured as instances of bipolar Assumption-Based Argumentation, a class of Assumption-Based Argumentation (ABA). In this paper, we establish the complexity of bipolar ABA, and consequently of several classes of BAFs. In addition to the standard five complexity problems, we analyse the rarely-addressed extension enumeration problem too. We also advance backtracking-driven algorithms for enumerating extensions of bipolar ABA frameworks, and consequently of BAFs under several interpretations. We prove soundness and completeness of our algorithms, describe their implementation and provide a scalability evaluation. We thus contribute to the study of the as yet uninvestigated complexity problems of (variously interpreted) BAFs as well as of bipolar ABA, and provide the lacking implementations thereof.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge