Complexity of Linear Minimization and Projection on Some Sets
Paper and Code
Jan 25, 2021
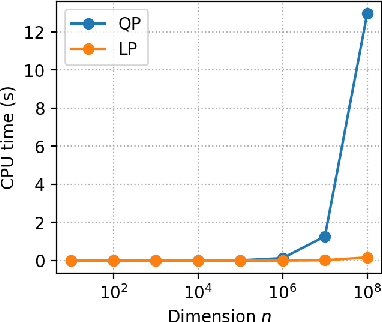
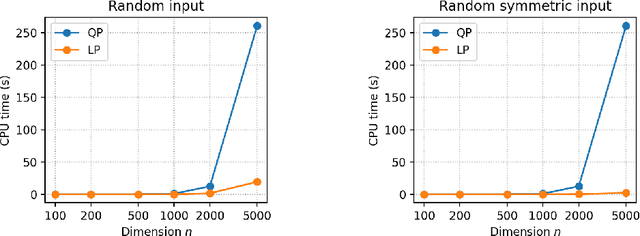
The Frank-Wolfe algorithm is a method for constrained optimization that relies on linear minimizations, as opposed to projections. Therefore, a motivation put forward in a large body of work on the Frank-Wolfe algorithm is the computational advantage of solving linear minimizations instead of projections. However, the discussions supporting this advantage are often too succinct or incomplete. In this paper, we review the complexity bounds for both tasks on several sets commonly used in optimization. Projection methods onto the $\ell_p$-ball, $p\in\left]1,2\right[\cup\left]2,+\infty\right[$, and the Birkhoff polytope are also proposed.
* 14 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge