Complexity and mission computability of adaptive computing systems
Paper and Code
Aug 29, 2018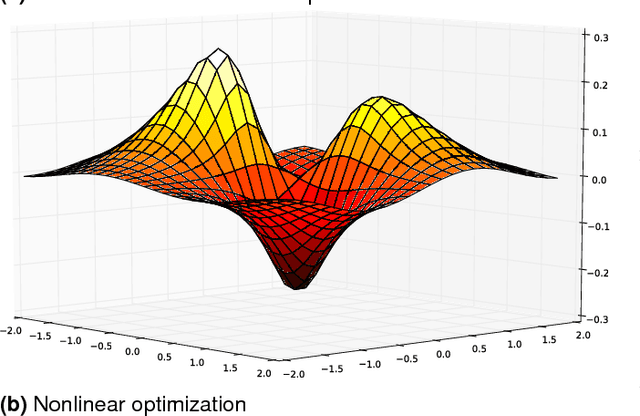
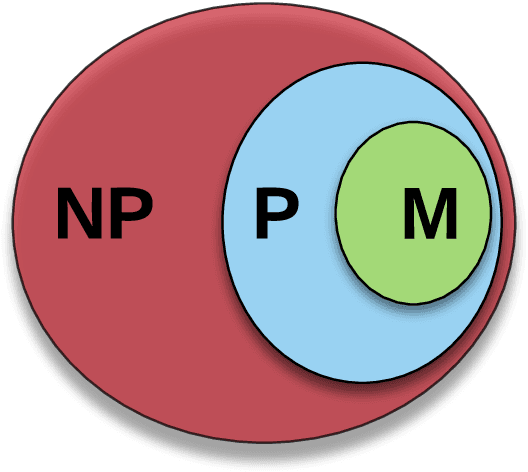
There is a subset of computational problems that are computable in polynomial time for which an existing algorithm may not complete due to a lack of high performance technology on a mission field. We define a subclass of deterministic polynomial time complexity class called mission class, as many polynomial problems are not computable in mission time. By focusing on such subclass of languages in the context for successful military applications, we also discuss their computational and communicational constraints. We investigate feasible (non)linear models that will minimize energy and maximize memory, efficiency, and computational power, and also provide an approximate solution obtained within a pre-determined length of computation time using limited resources so that an optimal solution to a language could be determined.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge